User:Wcherowi/sandbox
An example of a diff is this.

References[edit]
- Cherowitzo, William (1988), "Hyperovals in Desarguesian planes of even order", Ann. Discrete Math., 37: 87–94, MR 0931308
- Cherowitzo, W. (1996), "Hyperovals in Desarguesian planes: an update", Discrete Math., 155 (1–3): 31–38, doi:10.1016/0012-365X(94)00367-R, MR 1401356
- Cherowitzo, W. (1998), "α-flocks and hyperovals", Geom. Dedicata, 72 (3): 221–246, doi:10.1023/A:1005022808718, MR 1647703
- Cherowitzo, William E.; O'Keefe, Christine M.; Penttila, Tim (2003), "A unified construction of finite geometries associated with q-clans in characteristic 2", Adv. Geom., 3 (1): 1–21, doi:10.1515/advg.2003.002, MR 1956585
- Cherowitzo, W.; Penttila, T.; Pinneri, I.; Royle, G. F. (1996), "Flocks and ovals", Geom. Dedicata, 60 (1): 17–37, doi:10.1007/BF00150865, MR 1376478
- Glynn, David G. (1983), "Two new sequences of ovals in finite Desarguesian planes of even order", (Combinatorial mathematics, X) Lecture Notes in Math., vol. 1036, Berlin: Springer, pp. 217–229, MR 0731584
- Hirschfeld, J. W. P. (1998), Projective geometries over finite fields (2nd ed.), New York: The Clarendon Press Oxford University Press, pp. xiv+555, ISBN 0-19-850295-8, MR 1612570
- Korchmáros, G. (1978), "Collineation groups transitive on the points of an oval [q+2-arc] of S2,q for q even", Atti Sem. Mat. Fis. Univ. Modena (in Italian and with English summary), 27 (1): 89–105 (1979), MR 0551092
{{citation}}: CS1 maint: unrecognized language (link)
- Korchmáros, G. (1991), "Old and new results on ovals in finite projective planes", (Surveys in combinatorics, 1991) London Math. Soc. Lecture Note Ser., vol. 166, Cambridge: Cambridge Univ. Press, pp. 41–72, MR 1161460
- O'Keefe, Christine M.; Penttila, Tim (1992), "A new hyperoval in PG(2,32)", J. Geom., 44 (1–2): 117–139, doi:10.1007/BF01228288, MR 1169414
- Payne, Stanley E. (1985), "A new infinite family of generalized quadrangles", Congressus Numerantium, 49: 115–128, MR 0830735
- Penttila, Tim; Pinneri, Ivano (1994), "Irregular hyperovals in PG(2,64)", J. Geom., 51 (1–2): 89–100, doi:10.1007/BF01226860, MR 1298348
- Penttila, Tim; Royle, Gordon F. (1994), "Classification of hyperovals in PG(2,32)", J. Geom., 50 (1–2): 151–158, doi:10.1007/BF01222672, MR 1280636
- Penttila, Tim; Royle, Gordon F. (1995), "On hyperovals in small projective planes", J. Geom., 54 (1–2): 91–104, doi:10.1007/BF01222857, MR 1358279
- Segre, Beniamino (1962), "Ovali e curve σ nei piani di Galois di caratteristica due.", Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat. (8) (in Italian), 32: 785–790, MR 0149361
- Segre, B.; Bartocci, U. (1971), "Ovali ed altre curve nei piani di Galois di caratteristica due", Acta Arith. (in Italian), 18: 423–449, MR 0295201
In Geometry, collinearity is a property of a set of points, specifically, the property of lying on a single line.[1] A set of points with this property is said to be collinear (often misspelled as, but should not be confused with, co-linear or colinear). The term collinear has been used, in a generalized sense, both in mathematics and in its application areas, as a synonym for "aligned" or the expression "in a row".
Points on a line[edit]
In most geometries a line is a primitive (undefined) object type. A model for the geometry supplies an interpretation of what points, lines and other object types are. This abstract point of view requires a richer vocabulary to describe its concepts than does Euclidean geometry. Thus, in spherical geometry where lines are represented in the standard model by great circles of a sphere, sets of collinear points are those which lie on the same great circle. Such points do not lie on a "straight line" in the Euclidean sense and would not be thought of as being "in a row". Of course, if the geometry is Euclidean, then collinear points will lie on a straight line.
Linear maps (or linear functions), as geometric maps, are those which preserve the collinearity property (that is, they map collinear point sets to collinear point sets) which is another way to say that they map lines to lines.
Concurrency (plane dual)[edit]
In various plane geometries the notion of interchanging the roles of "points" and "lines" while preserving the relationship between them is called plane duality. Given a set of collinear points, by plane duality we obtain a set of lines all of which meet at a common point. The property that this set of lines has (meeting at a common point) is called concurrency, and the lines are said to be concurrent lines. Thus, concurrency is the plane dual notion to collinearity.
Collinear vs. co-linear[edit]
Duality has a broader meaning in mathematics than it has in just geometry. Often, the prefix "co-" is used to indicate that an object is the dual, in some sense, of some other object. Over time, the hyphen in this usage tends to disappear. Thus we find that in coalgebra theory, the notion of a colinear map (or co-linear map) is dual to the notion of a linear map for vector spaces.
Collinearity graph[edit]
Given a partial geometry P, where two points determine at most one line, a collinearity graph of P is a graph whose vertices are the points of P, where two vertices are adjacent if and only if they determine a line in P.
Usage in statistics and econometrics[edit]
In Statistics, collinearity refers to a linear relationship between two explanatory variables. Two variables are perfectly collinear if there is an exact linear relationship between the two. For example, and are perfectly collinear if there exist parameters and such that, for all observations i, we have
Multicollinearity refers to a situation in which two or more explanatory variables in a multiple regression model are highly linearly related. We have perfect multicollinearity if, for example as in the equation above, the correlation between two independent variables is equal to 1 or -1. In practice, we rarely face perfect multicollinearity in a data set. More commonly, the issue of multicollinearity arises when there is a strong linear relationship among two or more independent variables.
Mathematically, a set of variables is perfectly multicollinear if there exist one or more exact linear relationships among some of the variables.
Usage in other areas[edit]
Antenna arrays[edit]

In telecommunications, a collinear (or co-linear) antenna array is an array of dipole antennas mounted in such a manner that the corresponding elements of each antenna are parallel and aligned, that is they are located along a common line or axis.
Photography[edit]
The collinearity equations are a set of two equations, used in photogrammetry and remote sensing to relate coordinates in an image (sensor) plane (in two dimensions) to object coordinates (in three dimensions). In the photography setting, the equations are derived by considering the central projection of a point of the object through the optical centre of the camera to the image in the image (sensor) plane. The three points, object point, image point and optical centre, are always collinear. Another way to say this is that the line segments joining the object points with their image points are all concurrent at the optical centre.[2]
Notes[edit]
- ^ The concept applies in any geometry Dembowski (1968, pg. 26) harvtxt error: multiple targets (2×): CITEREFDembowski1968 (help), but is often only defined within the discussion of a specific geometry Coxeter (1969, pg. 168), Brannan, Esplen & Gray (1998, pg.106)
- ^ It would be more mathematically natural to refer to these equations as the "concurrency equations", but this terminology is not used in the photogrammetry literature.
References[edit]
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), Geometry, Cambridge: Cambridge University Press, ISBN 0-521-59787-0
- Coxeter, H. S. M. (1969), Introduction to Geometry, New York: John Wiley & Sons, ISBN 0-471-50458-0
- Dembowski, Peter (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, MR 0233275
In combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points (by Fisher's inequality). They have also been referred to as projective designs[1] or square designs.[2]
That is, a symmetric design is a (v,b,r,k,λ)-design with b = v and r = k. Either of the latter two equations implies the other. In fact, the parameters of a symmetric design satisfy
Clearly, this imposes strong restrictions on v, so the number of points is far from arbitrary. The Bruck–Ryser–Chowla theorem gives necessary but not sufficient conditions.
A theorem of Ryser gives a different combinatorial condition for an incidence structure to be symmetric. If X is a v-element set (the "point set"), and B is a v-element class of k-element subsets (called "blocks"), and any two blocks have exactly λ points in common, then (X, B) is a symmetric design.[3]
Examples[edit]
Examples include finite projective planes (λ = 1) and biplane geometries (λ = 2).
The order of a symmetric design is defined to be ;[1] For example, an order N projective plane has the terminology is because the projective plane over a field of q elements has lines with points.
See also[edit]
Notes[edit]
- ^ a b Nonexistence Proofs for Projective Designs, E. F. Assmus, Jr and David P. Maher, The American Mathematical Monthly, Vol. 85, No. 2 (Feb., 1978), pp. 110–112
- ^ These alternatives have been used in an attempt to replace the term "symmetric", since there is nothing symmetric (in the usual meaning of the term) about these designs. The use of projective is due to P.Dembowski (Finite Geometries, Springer, 1968) in analogy with the most common example, projective planes, while square is due to P. Cameron (Designs, Graphs, Codes and their Links, Cambridge, 1991) and captures the implication of v = b on the incidence matrix. Neither term has caught on as a replacement and these designs are still universally referred to as symmetric.
- ^ Ryser 1963, pp. 102-104
References[edit]
- Lander, E. S. (1983), Symmetric Designs: An Algebraic Approach, Cambridge: Cambridge University Press
- Ryser, Herbert John (1963), "Chapter 8: Combinatorial Designs", Combinatorial Mathematics (Carus Monograph #14), Mathematical Association of America
- Stinson, Douglas R. (2003). "Chapter 2: Symmetric BIBDs". Combinatorial Designs. New York: Springer-Verlag. ISBN 0-387-95487-2.
- Street, Anne Penfold and Street, Deborah J. (1987). Combinatorics of Experimental Design. Oxford U. P. [Clarendon]. pp. 400+xiv. ISBN 0-19-853256-3.
{{cite book}}: CS1 maint: multiple names: authors list (link)
- van Lint, J.H., and R.M. Wilson (1992), A Course in Combinatorics. Cambridge, Eng.: Cambridge University Press.
External links[edit]
- Design DB: A database of combinatorial, statistical, experimental block designs
In projective geometry, a von Staudt conic is the point set defined by all the absolute points of a polarity that has absolute points. In the real projective plane a von Staudt conic is a conic section in the usual sense. In more general projective planes this is not always the case. Karl Georg Christian von Staudt introduced this definition in Geometrie der Lage (1847) as part of his attempt to remove all metrical concepts from projective geometry.
Polarities[edit]
A polarity, π, of a projective plane, P, is an involutory (i.e., of order two) bijection between the points and the lines of P that preserves the incidence relation. Thus, a polarity relates a point Q with a line q and, following Gergonne, q is called the polar of Q and Q the pole of q.[1] An absolute point (line) of a polarity is one which is incident with its polar (pole).[2][3]
A polarity may or may not have absolute points. A polarity with absolute points is called a hyperbolic polarity and one without absolute points is called an elliptic polarity.[4] In the complex projective plane all polarities are hyperbolic but in the real projective plane only some are.[4]
A classification of polarities over arbitrary fields follows from the classification of sesquilinear forms given by Birkhoff and von Neumann.[5] Orthogonal polarities, corresponding to symmetric bilinear forms, are also called ordinary polarities and the locus of absolute points forms a non-degenerate conic (set of points whose coordinates satisfy an irreducible homogeneous quadratic equation) if the field does not have characteristic two. In characteristic two the orthogonal polarities are called psuedopolarities and in a plane the absolute points form a line.[6]
Finite projective planes[edit]
If π is a polarity of a finite projective plane (which need not be desarguesian), P, of order n then the number of its absolute points (or absolute lines), a(π) is given by:
- a(π) = n + 2r√n + 1,
where r is a non-negative integer.[7] Since a(π) is an integer, a(π) = n + 1 if n is not a square, and in this case, π is called an orthogonal polarity.
R. Baer has shown that if n is odd, the absolute points of an orthogonal polarity form an oval (that is, n + 1 points, no three collinear), while if n is even, the absolute points lie on a non-absolute line.[8]
In summary, von Staudt conics are not ovals in finite projective planes (desarguesian or not) of even order.[9][10]
Relation to other types of conics[edit]
In a pappian plane (i.e., a projective plane coordinatized by a field), if the field does not have characteristic two, a von Staudt conic is equivalent to a Steiner conic.[11] However, R. Artzy has shown that these two definitions of conics can produce non-isomorphic objects in (infinite) Moufang planes.[12]
Notes[edit]
- ^ Coxeter 1964, p. 60
- ^ Garner 1979, p. 132
- ^ Coxeter and several other authors use the term self-conjugate instead of absolute.
- ^ a b Coxeter 1964, p. 72
- ^ Birkhoff, G.; von Neumann, J. (1936), "The logic of quantum mechanics", Ann. Math., 37: 823–843
- ^ Barwick, Susan; Ebert, Gary (2008), Unitals in Projective Planes, Springer, pp. 16–18, ISBN 978-0-387-76364-4
- ^ Ball, R.W. (1948), "Dualities of Finite Projective Planes", Duke Mathematics Journal, 15: 929–940
- ^ Baer, Reinhold (1946), "Polarities in Finite Projective Planes", Bulletin of the American Mathematical Society, 52: 77–93
- ^ Garner 1979, p. 133
- ^ Dembowski 1968, pp. 154–155 harvnb error: multiple targets (2×): CITEREFDembowski1968 (help)
- ^ Coxeter 1964, p. 80
- ^ Artzy, R. (1971), "The Conic y = x2 in Moufang Planes", Aequationes Mathematica, 6: 30–35
References[edit]
- Dembowski, Peter (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, MR 0233275
- Garner, Cyril W L. (1979), "Conics in Finite Projective Planes", Journal of Geometry, 12 (2): 132–138
Further reading[edit]
- Ostrom, T.G. (1981), "Conicoids: Conic-like figures in Non-Pappian planes", in Plaumann, Peter; Strambach, Karl (eds.), Geometry - von Staudt's Point of View, D. Reidel, pp. 175–196, ISBN 90-277-1283-2
French quote[edit]
Et cette proposition est généralement vraie en toutes progressions et en tous nombres premiers; de quoi je vous envoierois la démonstration, si je n'appréhendois d'être trop long.
History[edit]
The birth of the concept of constructible numbers is inextricably linked with the history of the three impossible compass and straightedge constructions: duplicating the cube, trisecting an angle and squaring the circle. The restriction of using only compass and straightedge in geometric constructions is often credited to Plato due to a passage in Plutarch. According to Plutarch, Plato gave the duplication of the cube (Delian) problem to Eudoxus and Archytas and Menaechmus, who solved the problem using mechanical means, earning a rebuke from Plato for not solving the problem using pure geometry (Plut., Quaestiones convivales VIII.ii, 718ef). However, this attribution is challenged,[1] due, in part, to the existence of another version of the story (attributed to Eratosthenes by Eutocius of Ascalon) that says that all three found solutions but they were too abstract to be of practical value.[2] Since Oenopides (circa 450 BCE) is credited with two ruler and compass constructions, by Proclus– citing Eudemus (circa 370 - 300 BCE)–when other methods were available to him, has lead some authors to hypothesize that Oenopides originated the restriction.
The restriction to compass and straightedge is essential in making these constructions impossible. Angle trisection, for instance, can be done in many ways, several known to the ancient Greeks. The Quadratrix of Hippias of Elis, the conics of Menaechmus, or the marked straightedge (neusis) construction of Archimedes have all been used and we can add a more modern approach via paper folding to the list.
Although not one of the classic three construction problems, the problem of constructing regular polygons with straightedge and compass is usually treated alongside them. The Greeks knew how to construct regular n-gons with n = 2h, 3, 5 (for any integer h ≥ 2) or the product of any two or three of these numbers, but other regular n-gons eluded them. Then, in 1796, an eighteen-year-old student named Carl Friedrich Gauss announced in a newspaper that he had constructed a regular 17-gon with straightedge and compass.[3] Gauss' treatment was algebraic rather than geometric, in fact, he did not actually construct the polygon, but rather showed that the cosine of a central angle was a constructible number. The argument was generalized in his 1801 book Disquisitiones Arithmeticae giving the sufficient condition for the construction of a regular n-gon. Gauss claimed, but did not prove, that the condition was also necessary and several authors, notably Felix Klein,[4] attributed this part of the proof to him as well.[5]
In a paper from 1837,[6] Pierre Laurent Wantzel proved algebraically that the problems of
- doubling the cube, and
- trisecting the angle
are impossible to solve if one uses only compass and straightedge. In the same paper he also solved the problem of determining which regular polygons are constructible:
- a regular polygon is constructible if and only if the number of its sides is the product of a power of two and any number of distinct Fermat primes (i.e. that the sufficient conditions given by Gauss are also necessary)
An attempted proof of the impossibility of squaring the circle was given by James Gregory in Vera Circuli et Hyperbolae Quadratura (The True Squaring of the Circle and of the Hyperbola) in 1667. Although his proof was faulty, it was the first paper to attempt to solve the problem using algebraic properties of π. It was not until 1882 that Ferdinand von Lindemann rigorously proved its impossibility, by extending the work of Charles Hermite and proving that π is a transcendental number.
Combinatorics[edit]
Combinatorics, it has been said, "may rightly be called the mathematics of counting."[7] Few, however, would take this as a definition without a great deal of further amplification. Agreement on how this amplification should proceed is lacking and, according to Ryser (1963, p. 2), a definition of this subject is difficult because it crosses so many mathematical subdivisions. In so far as an area can be described by the types of problems it addresses, combinatorics is involved with
- the enumeration (counting) of specified structures, sometimes referred to as arrangements or configurations, associated with finite sets,
- the existence of such structures that satisfy certain given criteria,
- the construction of these structures, perhaps in many ways, drawing upon ideas from several areas of mathematics, and
- optimization, finding the "best" structure or solution among several possibilities, be it the "largest", "smallest" or satisfying some other optimality criterion.
Perhaps the easiest way to give an accounting of what combinatorics is, is to describe its subdivisions with their problems and techniques as is done below. However, even this approach is not completely satisfactory since it does not capture the purely historical reasons for including or not including some topics under the combinatorics umbrella.
Although primarily concerned with finite sets, some combinatorial questions and techniques can be extended to an infinite (specifically, countable) but discrete setting. This concentration on finite sets implies that techniques used in combinatorial arguments are more likely to be drawn from algebra than analysis.
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size (enumerative combinatorics), deciding when certain criteria can be met, and constructing and analyzing objects
meeting the criteria (as in combinatorial designs and matroid theory), finding "largest", "smallest", or "optimal" objects (extremal combinatorics and combinatorial optimization), and studying combinatorial structures arising in an algebraic context, or applying algebraic techniques to combinatorial problems (algebraic combinatorics).
______________________________________________
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics, from evolutionary biology to computer science, etc.
To fully understand the scope of combinatorics requires a great deal of further amplification, the details of which are not universally agreed upon.[8] According to H. J. Ryser, a definition of the subject is difficult because it crosses so many mathematical subdivisions.[9] In so far as an area can be described by the types of problems it addresses, combinatorics is involved with
- the enumeration (counting) of specified structures, sometimes referred to as arrangements or configurations in a very general sense, associated with finite systems,
- the existence of such structures that satisfy certain given criteria,
- the construction of these structures, perhaps in many ways, drawing upon ideas from several areas of mathematics, and
- optimization, finding the "best" structure or solution among several possibilities, be it the "largest", "smallest" or satisfying some other optimality criterion.
Leon Mirsky has said: "combinatorics is a range of linked studies which have something in common and yet diverge widely in their objectives, their methods, and the degree of coherence they have attained."[10] One way to define combinatorics is, perhaps, to describe its subdivisions with their problems and techniques. This is the approach that is used below. This approach is not completely satisfactory since it does not capture the purely historical reasons for including or not including some topics under the combinatorics umbrella. Although primarily concerned with finite systems, some combinatorial questions and techniques can be extended to an infinite (specifically, countable) but discrete setting.
Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry,[11] as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ad hoc solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics is graph theory, which by itself has numerous natural connections to other areas. Combinatorics is used frequently in computer science to obtain formulas and estimates in the analysis of algorithms.
A mathematician who studies combinatorics is called a combinatorialist or a combinatorist.
References
- ^ Kazarinoff 2003, p. 28
- ^ Knorr, Wilbur Richard (1986), The Ancient Tradition of Geometric Problems, Dover Books on Mathematics, Courier Dover Publications, p. 4, ISBN 9780486675329.
- ^ Kazarinoff 2003, p. 29
- ^ Klein, Felix (1956) [1930], Famous Problems of Elementary Geometry, Dover, p. 16
- ^ Kazarinoff 2003, p. 30
- ^ Wantzel, P. L. (1837), "Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas", Journal de Mathématiques Pures et Appliquées, 1 (2): 366–372
- ^ Mazur 2010, pg. vii
- ^ Pak, Igor. "What is Combinatorics?". Retrieved 1 November 2017.
- ^ Ryser 1963, p. 2
- ^ Mirsky, Leon (1979), "Book Review" (PDF), Bulletin (New Series) of the American Mathematical Society, 1: 380–388
- ^ Björner and Stanley, p. 2
Affine transformation[edit]

In geometry, an affine transformation, or an affinity (from the Latin, affinis, "connected with") is an automorphism of an affine space. More specifically, it is a function mapping an affine space onto itself that preserves the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and also preserves the ratio of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line.
If X is the point set of an affine space, then every affine transformation on X can be represented as the composition of a linear transformation on X and a translation of X. Unlike a purely linear transformation, an affine transformation need not preserve the origin of the affine space. Thus, every linear transformation is affine, but not every affine transformation is linear.
Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination and sequence.
Viewing an affine space as the compliment of a hyperplane at infinity of a projective space, the affine transformations are the projective transformations of that projective space that leave the hyperplane at infinity invariant, restricted to the compliment of that hyperplane.
A generalization of an affine transformation is an affine map[1] (or affine homomorphism or affine mapping) between two affine spaces, over the same field k, which need not be the same. Let (X, V, k) and (Z, W, k) be two affine spaces with X and Z the point sets and V and W the respective associated vector spaces over the field k. A map f: X → Z is an affine map if there exists a linear map mf : V → W such that mf (x − y) = f (x) − f (y) for all x, y in X.[2]
Definition[edit]
Let (X, V, k) be an affine space of dimension at least two, with X the point set and V the associated vector space over the field k. A semiaffine transformation f of X is a bijection of X onto itself satisfying:[3]
- If S is a d-dimensional affine subspace of X, f (S) is also a d-dimensional affine subspace of X.
- If S and T are parallel affine subspaces of X, then f (S) || f (T).
These two conditions express what is precisely meant by the expression that "f preserves parallelism".
These conditions are not independent as the second follows from the first.[4] Furthermore, if the field k has at least three elements, the first condition can be simplified to: f is a collineation, that is, it maps lines to lines.[5]
If the dimension of the affine space (X, V, k) is at least two, then an affine transformation is a semiaffine transformation f that satisfies the condition: If x ≠ y and p ≠ q are points of X such that the line segments xy and pq are parallel, then[6]
Affine lines[edit]
If the dimension of the affine space is one, that is, the space is an affine line, then any permutation of X would automatically satisfy the conditions to be a semiaffine transform. So, an affine transformation of an affine line is defined as any permutation f of the points of X such that if x ≠ y and p ≠ q are points of X, then[7]
Structure[edit]
By the definition of an affine space, V acts on X, so that, for every pair (x, v) in X × V there is associated a point y in X. We can denote this action by v→(x) = y. Here we use the convention that v→ = v are two interchangeable notations for an element of V. By fixing a point c in X one can define a function mc : X → V by mc(x) = cx→. For any c, this function is one-to-one, and so, has an inverse function mc-1 : V → X given by mc-1(v) = v→(c). These functions can be used to turn X into a vector space (with respect to the point c) by defining:[8]
- and
This vector space has origin c and formally needs to be distinguished from the affine space X, but common practice is to denote it by the same symbol and mention that it is a vector space after an origin has been specified. This identification permits points to be viewed as vectors and vice versa.
For any linear transformation λ of V, we can define the function L(c, λ) : X → X by
Then L(c, λ) is an affine transformation of X which leaves the point c fixed.[9] It is a linear transformation of X, viewed as a vector space with origin c.
Let σ be any affine transformation of X. Pick a point c in X and consider the translation of X by the vector , denoted by Tw. Translations are affine transformations and the composition of affine transformations is an affine transformation. For this choice of c, there exists a unique linear transformation λ of V such that[10]
That is, an arbitrary affine transformation of X is the composition of a linear transformation of X (viewed as a vector space) and a translation of X.
This representation of affine transformations is often taken as the definition of an affine transformation (with the choice of origin being implicit).[11][12][13]
All Euclidean spaces are affine, but there are affine spaces that are non-Euclidean. In affine coordinates, which include Cartesian coordinates in Euclidean spaces, each output coordinate of an affine map is a linear function (in the sense of calculus) of all input coordinates. Another way to deal with affine transformations systematically is to select a point as the origin; then, any affine transformation is equivalent to a linear transformation (of position vectors) followed by a translation.
Cosets[edit]
In mathematics, specifically group theory, a subgroup H of a group G may be used to decompose the underlying set of G into disjoint equal size pieces called cosets. There are two types of cosets, left cosets and right cosets. Cosets (of either type) have the same number of elements (cardinality) as does H. Furthermore, H itself is a coset, which is both a left coset and a right coset. The number of left cosets of H in G is equal to the number of right cosets of H in G. The common value is called the index of H in G and is usually denoted by [G : H].
Cosets are a basic tool in the study of groups; for example they play a central role in Lagrange's theorem that states that for any finite group G, the number of elements of every subgroup H of G divides the number of elements of G. Cosets of a particular type of subgroup (normal subgroup) can be used as the elements of another group called a quotient group or factor group. Cosets also appear in other areas of mathematics such as vector spaces and error-correcting codes.
Definition[edit]
Let H be a subgroup of the group G whose operation is written multiplicatively (juxtaposition means apply the group operation). Given an element g of G, then a left coset of H in G is obtained by multiplying each element of H by the fixed element g (where g is the left factor). In symbols this is,
- gH = { gh : h an element of H }.
Right cosets are defined similarly, except that the element g is now a right factor, that is,
- Hg = { hg : h an element of H }.
If the group operation is written additively, as is often the case when the group is abelian, the notation used changes to g + H or H + g, respectively.
Properties[edit]
Because H is a subgroup, it contains the group's identity element, with the result that the element g belongs to the coset gH. If x belongs to gH then xH=gH. Thus every element of G belongs to exactly one left coset of the subgroup H.
Elements g and x belong to the same left coset of H, that is, xH = gH if and only if g-1x belongs to H. More can be said here. Define two elements of G, say x and y, to be equivalent with respect to the subgroup H if x-1y belongs to H. This is then an equivalence relation on G and the equivalence classes of this relation are the left cosets of H. As with any set of equivalence classes, they form a partition of the underlying set.
Similar statements apply to right cosets.
If G is an abelian group, then gH = Hg for every subgroup H of G and every element g of G. In general, given an element g and a subgroup H of a group G, the right coset of H with respect to g is also the left coset of the conjugate subgroup g−1Hg with respect to g, that is, Hg = g ( g−1Hg ).
A subgroup N of a group G is a normal subgroup of G if and only if for all elements g of G the corresponding left and right cosets are equal, that is, gN = Ng. Furthermore, the cosets of N in G form a group called the quotient group or factor group.
An application from coding theory[edit]
A binary linear code is an n-dimensional subspace C of an m-dimensional vector space V over the binary field GF(2). As V is an additive abelian group, C is a subgroup of this group. Codes can be used to correct errors that can occur in transmission. When a codeword (element of C) is transmitted some of its bits may be altered in the process and the task of the receiver is to determine the most likely codeword that the corrupted received word could have started out as. This procedure is called decoding and if only a few errors are made in transmission it can be done effectively with only a very few mistakes. One method used for decoding uses an arrangement of the elements of V (a received word could be any element of V) into a standard array. A standard array is a coset decomposition of V put into tabular form in a certain way. Namely, the top row of the array consists of the elements of C, written in any order, except that the zero vector should be written first. Then, an element of V with a minimal number of ones that does not already appear in the top row is selected and the coset of C containing this element is written as the second row (namely, the row is formed by taking the sum of this element with each element of C directly above it). This element is called a coset leader and there may be some choice in selecting it. Now the process is repeated, a new vector with a minimal number of ones that does not already appear is selected as a new coset leader and the coset of C containing it is the next row. The process ends when all the vectors of V have been sorted into the cosets.
An example of a standard array for the 2-dimensional code C = {00000, 01101, 10110, 11011} in the 5-dimensional space V (with 32 vectors) is as follows:
00000 01101 10110 11011 10000 11101 00110 01011 01000 00101 11110 10011 00100 01001 10010 11111 00010 01111 10100 11001 00001 01100 10111 11010 11000 10101 01110 00011 10001 11100 00111 01010
The decoding procedure is to find the received word in the table and then add to it the coset leader of the row it is in. Since in binary arithmetic adding is the same operation as subtracting, this always results in an element of C. In the event that the transmission errors occurred in precisely the non-zero positions of the coset leader the result will be the right codeword. In this example, if a single error occurs, the method will always correct it, since all possible coset leaders with a single one appear in the array.
Syndrome decoding can be used to improve the efficiency of this method. It is a method of computing the correct coset (row) that a received word will be in. For an n-dimensional code C in an m-dimensional binary vector space, a parity check matrix is an (m − n) × m matrix H having the property that H x→ = 0→ if and only if x→ is in C. The vector H x→ is called the syndrome of x→, and by linearity, every vector in the same coset will have the same syndrome. To decode, the search is now reduced to finding the coset leader that has the same syndrome as the received word.[14]
Mutually orthogonal Latin squares (MOLS)[edit]
A set of Latin squares of the same order such that every pair of squares are orthogonal (that is, form a Graeco-Latin square) is called a set of mutually orthogonal Latin squares and usually abbreviated as MOLS or MOLS(n) when the order is made explicit.
For example, a set of MOLS(4) is given by:[15]
And a set of MOLS(5):[16]
While it is possible to represent MOLS in a "compound" matrix form similar to the Graeco-Latin squares, for instance,
1,1,1,1 2,2,2,2 3,3,3,3 4,4,4,4 5,5,5,5 2,3,5,4 3,4,1,5 4,5,2,1 5,1,3,2 1,2,4,3 3,5,4,2 4,1,5,3 5,2,1,4 1,3,2,5 2,4,3,1 4,2,3,5 5,3,4,1 1,4,5,2 2,5,1,3 3,1,2,4 5,4,2,3 1,5,3,4 2,1,4,5 3,2,5,1 4,3,1,2
for the MOLS(5) example above, it is more typical to compactly represent the MOLS as an orthogonal array (see below).
Orthogonal array[edit]
An orthogonal array, OA(k,n), of strength two and index one is an n2 × k array A (k ≥ 2 and n ≥ 1, integers) with entries from a set of size n such that within any two columns of A, every ordered pair of symbols appears in exactly one row of A.[17]
An OA(s + 2, n) is equivalent to s MOLS(n).[17] For example, the MOLS(4) example given above and repeated here,
can be used to form an OA(5,4):
r c L1 L2 L3 1 1 1 1 1 1 2 2 2 2 1 3 3 3 3 1 4 4 4 4 2 1 2 4 3 2 2 1 3 4 2 3 4 2 1 2 4 3 1 2 3 1 3 2 4 3 2 4 1 3 3 3 1 4 2 3 4 2 3 1 4 1 4 3 2 4 2 3 4 1 4 3 2 1 4 4 4 1 2 3
where the entries in the columns labeled r and c denote the row and column of a position in a square and the rest of the row for fixed r and c values is filled with the entry in that position in each of the Latin squares. This process is reversible; given an OA(s,n) with s ≥ 3, choose any two columns to play the r and c roles and then fill out the Latin squares with the entries in the remaining columns.
Pencil (mathematics)[edit]

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.
Although the definition of a pencil is rather vague, the common characteristic is that the pencil is completely determined by any two of its members. Analogously, a set of geometric objects that are determined by any three of its members is called a bundle.[18] Thus, the set of all lines through a point in three-space is a bundle of lines, any two of which determine a pencil of lines. To emphasize the two dimensional nature of such a pencil, it is sometimes referred to as a flat pencil.
Any geometric object can be used in a pencil. The common ones are lines, planes, circles, conics, spheres and general curves. Even points can be used. A pencil of points is the set of all points on a given line.[18] A more common term for this set is a range of points.
Pencil of lines[edit]
In a plane, let u and v be two distinct intersecting lines. For concreteness, suppose that u has the equation, aX + bY + c = 0 and v has the equation a'X + b'Y + c′ = 0. Then
- λu + μv = 0,
represents, for suitable scalars λ and μ, any line passing through the intersection of u = 0 and v = 0. This set of lines passing through a common point is called a pencil of lines.[19] The common point of a pencil of lines is called the vertex of the pencil.
In an affine plane with the reflexive variant of parallelism, a set of parallel lines forms an equivalence class called a pencil of parallel lines.[20] This terminology is consistent with the above definition since in the unique projective extension of the affine plane to a projective plane a single point (point at infinity) is added to each line in the pencil of parallel lines, thus making it a pencil in the above sense in the projective plane.
Pencil of planes[edit]
A pencil of planes, is the set of planes through a given straight line in three-space, called the axis of the pencil. The pencil is sometimes referred to as a fan or a sheaf.[21] For example, the meridians of the globe are defined by the pencil of planes on the axis of Earth's rotation.
Two intersecting planes meet in a line in three-space, and so, determine the axis and hence all of the planes in the pencil.
In higher dimensional spaces, a pencil of hyperplanes consists of all the hyperplanes that contain a subspace of codimension 2. Such a pencil is determined by any two of its members.
Pencil of circles[edit]
Any two circles in the plane have a common radical axis, which is the line consisting of all the points that have the same power with respect to the two circles. A pencil of circles (or coaxial system) is the set of all circles in the plane with the same radical axis.[22] To be inclusive, concentric circles are said to have the line at infinity as a radical axis.
There are five types of pencils of circles,[23] the two families of Apollonian circles in the illustration above represent two of them. Each type is determined by two circles called the generators of the pencil. When described algebraically, it is possible that the equations may admit imaginary solutions. The types are:
- An elliptic pencil (red family of circles in the figure) is defined by two generators that pass through each other in exactly two points. Every circle of an elliptic pencil passes through the same two points. An elliptic pencil does not include any imaginary circles.
- A hyperbolic pencil (blue family of circles in the figure) is defined by two generators that do not intersect each other at any point. It includes real circles, imaginary circles, and two degenerate point circles called the Poncelet points of the pencil. Each point in the plane belongs to exactly one circle of the pencil.
- A parabolic pencil (as a limiting case) is defined where two generating circles are tangent to each other at a single point. It consists of a family of real circles, all tangent to each other at a single common point. The degenerate circle with radius zero at that point also belongs to the pencil.
- A family of concentric circles centered at a common center (may be considered a special case of a hyperbolic pencil where the other point is the point at infinity).
- The family of straight lines through a common point; these should be interpreted as circles that all pass through the point at infinity (may be considered a special case of an elliptic pencil).[24][25]
Properties[edit]
A circle that is orthogonal to two fixed circles is orthogonal to every circle in the pencil they determine.[26]
The circles orthogonal to two fixed circles form a pencil of circles.[26]
Two circles determine two pencils, the unique pencil that contains them and the pencil of circles orthogonal to them. The radical axis of one pencil consists of the centers of the circles of the other pencil. If one pencil is of elliptic type, the other is of hyperbolic type and vice versa.[26]
Projective space of circles[edit]
There is a natural correspondence between circles in the plane and points in three-dimensional projective space; a line in this space corresponds to a one-dimensional continuous family of circles, hence a pencil of points in this space is a pencil of circles in the plane.
Specifically, the equation of a circle of radius r centered at a point (p,q),
may be rewritten as
where α = 1, β = p, γ = q, and δ = p2 + q2 − r2. In this form, multiplying the quadruple (α,β,γ,δ) by a scalar produces a different quadruple that represents the same circle; thus, these quadruples may be considered to be homogeneous coordinates for the space of circles.[27] Straight lines may also be represented with an equation of this type in which α = 0 and should be thought of as being a degenerate form of a circle. When α ≠ 0, we may solve for p = β/α, q = γ/α, and r =√(p2 + q2 − δ/α); the latter formula may give r = 0 (in which case the circle degenerates to a point) or r equal to an imaginary number (in which case the quadruple (α,β,γ,δ) is said to represent an imaginary circle).
The set of affine combinations of two circles (α1,β1,γ1,δ1), (α2,β2,γ2,δ2), that is, the set of circles represented by the quadruple
for some value of the parameter z, forms a pencil; the two circles being the generators of the pencil.
Cardioid as envelope of a pencil of circles[edit]
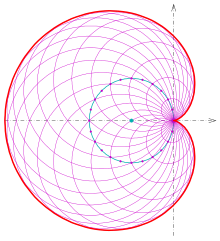
Another type of pencil of circles can be obtained as follows. Consider a given circle (called the generator circle) and a distinguished point P on the generator circle. The set of all circles that pass through P and have their centers on the generator circle form a pencil of circles. The envelope of this pencil is a cardioid.
Pencil of conics[edit]
A (non-degenerate) conic is completely determined by five points in general position (no three collinear) in a plane and the system of conics which pass through a fixed set of four points (again in a plane and no three collinear) is called a pencil of conics.[28] The four common points are called the base points of the pencil. Through any point other than a base point, there passes a single conic of the pencil. This concept generalizes a pencil of circles.
In a projective plane defined over an algebraically closed field any two conics meet in four points (counted with multiplicity) and so, determine the pencil of conics based on these four points. Furthermore, the four base points determine three line pairs (degenerate conics through the base points, each line of the pair containing exactly two base points) and so each pencil of conics will contain at most three degenerate conics.[29]
A pencil of conics can be represented algebraically in the following way. Let C1 and C2 be two distinct conics in a projective plane defined over an algebraically closed field K. For every pair λ, μ of elements of K, not both zero, the expression:
represents a conic in the pencil determined by C1 and C2. This symbolic representation can be made concrete with a slight abuse of notation (using the same notation to denote the object as well as the equation defining the object.) Thinking of C1, say, as a ternary quadratic form, then C1 = 0 is the equation of the "conic C1". Another concrete realization would be obtained by thinking of C1 as the 3×3 symmetric matrix which represents it. If C1 and C2 have such concrete realizations then every member of the above pencil will as well. Since the setting uses homogeneous coordinates in a projective plane, two concrete representations (either equations or matrices) give the same conic if they differ by a non-zero multiplicative constant.
Pencil of plane curves[edit]
More generally, a pencil is the special case of a linear system of divisors in which the parameter space is a projective line. Typical pencils of curves in the projective plane, for example, are written as
where C = 0, C′ = 0 are plane curves.
History[edit]
Desargues is credited with inventing the term "pencil of lines" (ordonnance de lignes).[30]
An early author of modern projective geometry G. B. Halsted introduced many terms, most of which are now considered to be archaic. For example, "Straights with the same cross are copunctal." Also "The aggregate of all coplanar, copunctal straights is called a flat-pencil" and "A piece of a flat-pencil bounded by two of the straights as sides, is called an angle."[31]
"The aggregate of all planes on a straight is called an axial-pencil."
See also[edit]
Notes[edit]
- ^ Berger 1987, p. 38.
- ^ Samuel 1988, p. 11.
- ^ Snapper & Troyer 1989, p. 65.
- ^ Snapper & Troyer 1989, p. 66.
- ^ Snapper & Troyer 1989, p. 69.
- ^ Snapper & Troyer 1989, p. 71.
- ^ Snapper & Troyer 1989, p. 72.
- ^ Snapper & Troyer 1989, p. 59.
- ^ Snapper & Troyer 1989, p. 76,87.
- ^ Snapper & Troyer 1989, p. 86.
- ^ Wan 1993, pp. 19–20.
- ^ Klein 1948, p. 70.
- ^ Brannan, Esplen & Gray 1999, p. 53.
- ^ Rotman 2006, p. 423
- ^ Colburn & Dinitz 2007, p. 160
- ^ Colburn & Dinitz 2007, p. 163
- ^ a b Stinson 2004, p. 140
- ^ a b Young 1971, p. 40
- ^ Pedoe 1988, p. 106
- ^ Artin 1957, p. 53
- ^ Woods 1961, p. 12
- ^ Johnson 2007, p. 34
- ^ Some authors combine types and reduce the list to three. Schwerdtfeger (1979, pp. 8–10)
- ^ Johnson 2007, p. 36
- ^ Schwerdtfeger 1979, pp. 8–10
- ^ a b c Johnson 2007, p. 37
- ^ Pfeifer & Van Hook 1993.
- ^ Faulkner 1952, pg. 64.
- ^ Samuel 1988, pg. 50.
- ^ Earliest Known Uses of Some Words of Mathematics, retrieved July 14, 2020
- ^ G. B. Halsted (1906) Synthetic Projective Geometry, page 9, via Internet Archive
References[edit]
- Artin, E. (1957), Geometric Algebra, Interscience Publishers
- Faulkner, T. E. (1952), Projective Geometry (2nd ed.), Edinburgh: Oliver and Boyd
- Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover, ISBN 978-0-486-46237-0
- Pedoe, Dan (1988) [1970], Geometry /A Comprehensive Course, Dover, ISBN 0-486-65812-0
- Pfeifer, Richard E.; Van Hook, Cathleen (1993), "Circles, Vectors, and Linear Algebra", Mathematics Magazine, 66 (2): 75–86, doi:10.2307/2691113, JSTOR 2691113
- Samuel, Pierre (1988), Projective Geometry, Undergraduate Texts in Mathematics (Readings in Mathematics), New York: Springer-Verlag, ISBN 0-387-96752-4
- Schwerdtfeger, Hans (1979) [1962], Geometry of Complex Numbers: Circle Geometry, Moebius Transformation, Non-Euclidean Geometry, Dover, pp. 8–10.
- Young, John Wesley (1971) [1930], Projective Geometry, Carus Monograph #4, Mathematical Association of America
- Woods, Frederick S. (1961) [1922], Higher Geometry / An introduction to advanced methods in analytic geometry, Dover

























