User:The Editor's Apprentice/sandbox/4

Not to be confused with parallel transport.

Parallel curves of the graph of ${\textstyle y=1.5\sin(x)}$ for distances ${\textstyle d=0.25,\dots ,1.5}$. Of note, although the sine curve is smooth, not all of its parallel curves are.

Cuts made by CNC wood router. Each cut has a pair of parallel curves as its boundaries.

In differential geometry, a parallel curve, also called an offset curve, is a generalization of the idea of parallel lines to all 2D curves. The concept further generalizes to 3D surfaces where it is called a parallel surface as well as an offset surface. Multiple mathematical definitions exist for parallel curves, not all of which are equivalent.The names "offset curve" and "offset surface" are particularly common in computer-aided design (CAD) and computer graphics contexts.

Parallel curves have multiple practical applications in fields including numerically controlled machining and computer graphics. In numerically controlled machining, they can be used to describe the shape cut out by a round cutting tool of a two-axis machine, such as a CNC wood router. In vector graphics, the approximation of parallel curves is involved in one of the fundamental drawing operations called "stroking". Stroking involves increasing the thicknesses of paths, typically polylines, a connected series of lines, or polybeziers, a connected series of Bézier curves.

Parallel surfaces are important in numerically controlled machining, where they describe the shape of the cut made by a ball-nose-end mill of a three-axis machine. Other shapes of cutting bits can be modeled mathematically by general parallel surfaces.

In most cases, a parallel curve does not maintain the same properties as its generating curve (the curve the parallel curve is based on). For example, even if a generating curve is smooth, its parallel curve may not be. Similarly, even if a curve is rational, such as an ellipse or hyperbola, its parallel curves generally are not so.

Definitions and terminology

Visual of two definitions of a parallel curve.

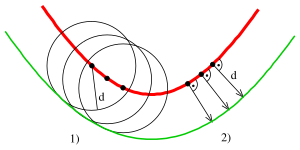
Parallel curves can be defined multiple ways, including:

1. the envelope of circles with fixed radii centered on a generating curve,
2. the locus of the points which are at a fixed, normal distance from a generating curve,
3. the locus of consecutive intersections of a system of congruent circles centered on a generating curve, and
4. the boundary of the Minkowski sum of a disk and an generating curve

The four definitions of a parallel curve are not always equivalent. For example, the first assumes smoothness of the generating function while the second does not. Additionally, the Minkowski addition based definition is only valid when the generating curve is a boundary of a planar set and its parallel curve is does not intersect itself.

A parallel surface with a greater volume than that of its generating surface is sometimes called "dilation" and the reverse is sometimes called a "shelling".

The variable $d$ is commonly used for the distance between a generating curve and a parallel curve.

General geometric properties

• Tangent vectors of a generating curve are parallel to the corresponding normal vectors of its parallel curve.
• Additionally, the same is true for the normal vectors of a generating and parallel curve.
• Parallel curves have cusps when the curvatures of the generating curve and the parallel curve are equal. The cusps are also points where the curve touches the evolute.
• The radii${\textstyle R_{d}(t)=R(t)+d,}$ where $R(t)$ and ${\textstyle R_{d}(t)}$ are respectively the radii of curvature of the generating and parallel curves.

• ${\textstyle k_{d}(t)={\frac {k(t)}{1+dk(t)}},}$ where ${\textstyle k(t)}$ and $k_{d}(t)$ are respectively the curvatures of the generating and the parallel curves.

Parametric curves

A regular parametric representation, ${\textstyle {\vec {x}}=(x(t),y(t))}$, of a curve using locus of points definition of leads to the following parametric representation of the parallel curve a distance ${\textstyle d}$ away:

${\vec {x}}_{d}(t)={\vec {x}}(t)+d{\vec {n}}(t)$

where ${\textstyle {\vec {n}}(t)}$ representing the unit normal vector of ${\textstyle {\vec {x}}}$ at ${\textstyle t}$.

Translated into Cartesian coordinates:

$x_{d}(t)=x(t)+{\frac {d\;y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}$

$y_{d}(t)=y(t)-{\frac {d\;x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}.$

In the cases when $d$ is negative, the parallel curve is on the opposite side of the generating curve than when $d$ is positive.

If the generating curve is polynomial, meaning that both $x(t)$ and $y(t)$ are polynomials, then the parallel curves are usually not polynomial. In the context of CAD, this is a drawback because CAD systems use polynomials or rational curves. In order to get at least rational curves, the square root of the representation of the parallel curve has to be solvable. Such curves are called "pythagorean hodograph curves" and were covered in detail by R.T. Farouki.

Implicit curves

Parallel curves of the implicit curve $x^{4}+y^{4}-1=0$, here shown in bright red.

Generally, the analytic representation of a parallel curve based on an implicit curve is not possible. Only for the simple cases of lines and circles the parallel curves can be described easily. For example, the line $f(x,y)=x+y-1=0$ has the distance function ${\textstyle h(x,y)={\frac {x+y-1}{\sqrt {2}}}=d}$ inHesse normal form. Similarly, the circle ${\textstyle f(x,y)=x^{2}+y^{2}-1=0}$ has the distance function ${\textstyle h(x,y)={\sqrt {x^{2}+y^{2}}}-1=d}$.

In general, presuming certain conditions, one can prove the existence of an oriented distance function $h(x,y)$, but in practice one has to treat it numerically.

Properties of the distance function

• The parallel curve for distance d is the level set $h(x,y)=d$ of the corresponding oriented distance function $h$,
• $|\operatorname {grad} h({\vec {x}})|=1$,
• $h({\vec {x}}+d\operatorname {grad} h({\vec {x}}))=h({\vec {x}})+d$,
• $\operatorname {grad} h({\vec {x}}+d\operatorname {grad} h({\vec {x}}))=\operatorname {grad} h({\vec {x}})$.

Of note, the curves $f(x,y)=x^{4}+y^{4}-1=d$ are not parallel curves of $f(x,y)=x^{4}+y^{4}-1=0$ because $|\operatorname {grad} f(x,y)|\neq 1$ in the area of interest.

Specific cases

Involutes of a circle, each of which is a parallel curve to the others.

• The involutes of an generating curve are a set of parallel curves. For example: the involutes of a circle are parallel spirals.

The following is true about the parallel curves of certain generating functions:

• A parabola has as (two-sided) offsets rational curves of degree 6.
• A hyperbola or an ellipse has as (two-sided) offsets an algebraic curve of degree 8.
• A Bézier curve of degree n has as (two-sided) offsets algebraic curves of degree 4n − 2. In particular, a cubic Bézier curve has as (two-sided) offsets algebraic curves of degree 10.
• More information at http://web.archive.org/web/20160303214952/http://www3.uah.es/fsegundo/Otros/Offset/16-SanSegundoSendraSendra-1532.pdf

Corners

Parallel curves to a curve with a discontinuous normal around a corner

When determining the cutting path of part with a sharp corner for machining, a parallel curve needs to defined which accommodates the discontinuous normal of the generating curve at the corner. Even though the generating curve is not smooth at the sharp corner, its parallel curve may be smooth with a continuous normal, or it may have may have cusps when the distance from the curve matches the radius of curvature at the sharp corner.

Normal fans

Normal fan for defining parallel curves around a sharp corner

As described in the section on parametric curves, the parametric representation of a parallel curve, ${\vec {x}}_{d}(t)$, to a generating curve, ${\vec {x}}(t)$, with distance $d$ is:

${\vec {x}}_{d}(t)={\vec {x}}(t)+d{\vec {n}}(t)$ with the unit normal ${\vec {n}}(t)$.

At a sharp corner, for example where $t=t_{c}$, the normal to ${\vec {x}}(t_{c})$ is undefined. This is because ${\vec {n}}(t)$ has a jump discontinuity at $t_{c}$. Specifically, the one-sided limit of the normal from the left, ${\vec {n}}(t_{c}^{-})$, is unequal to the limit from the right, ${\vec {n}}(t_{c}^{+})$. Mathematically,

$${\vec {n}}(t_{c}^{-})=\lim _{t\to t_{c}^{-}}{\vec {n}}(t)\neq \lim _{t\to t_{c}^{+}}{\vec {n}}(t)={\vec {n}}(t_{c}^{+})$$

.

A normal fan ${\vec {n}}_{f}(\alpha )$ can be used in the interpolate between ${\vec {n}}(t_{c}^{-})$ and ${\vec {n}}(t_{c}^{+})$ by being used in place of ${\vec {n}}(t_{c})$ at the sharp corner in the definition of ${\vec {x}}_{d}(t).$ Such a normal fan is defined as

${\vec {n}}_{f}(\alpha )={\frac {(1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\vec {n}}(t_{c}^{+})}{\lVert (1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\vec {n}}(t_{c}^{+})\rVert }},\quad$where $0<\alpha <1$.

The resulting definition of the parallel curve ${\vec {x}}_{d}(t)$ incorporating the normal fan is

${\vec {x}}_{d}(t)={\begin{cases}{\vec {x}}(t)+d{\vec {n}}(t),&{\text{if }}t<t_{c}{\text{ or }}t>t_{c}\\{\vec {x}}(t_{c})+d{\vec {n}}_{f}(\alpha ),&{\text{if }}t=t_{c}{\text{ where }}0<\alpha <1\end{cases}}.$

Algorithms

An efficient algorithm for offsetting is the level approach described by Kimel and Bruckstein (1993).

There are numerous approximation algorithms for this problem, cf. Elber et. al. 1997.

Parallel surfaces

Parallel surface of an irregular shape.

parallel surfaces are important in numerically controlled machining, where they describe the shape of the cut made by a ball nose end mill of a three-axis mill. If there is a regular parametric representation ${\vec {x}}(u,v)=(x(u,v),y(u,v),z(u,v))$ of the generating surface available, the second definition of a parallel curve (see above) generalizes to the following parametric representation of the parallel surface with distance $|d|$:

${\vec {x}}_{d}(u,v)={\vec {x}}(u,v)+d{\vec {n}}(u,v)$ with the unit normal ${\vec {n}}_{d}(u,v)={{{\partial {\vec {x}} \over \partial u}\times {\partial {\vec {x}} \over \partial v}} \over {|{{\partial {\vec {x}} \over \partial u}\times {\partial {\vec {x}} \over \partial v}}|}}$.

Distance parameter $d$ may be negative, too. In this case one gets a parallel surface on the opposite side of the surface (see similar diagram on the parallel curves of a circle). One easily checks: a parallel surface of a plane is a parallel plane in the common sense and the parallel surface of a sphere is a concentric sphere.

Geometric properties

• ${\partial {\vec {x}}_{d} \over \partial u}\parallel {\partial {\vec {x}} \over \partial u},\quad {\partial {\vec {x}}_{d} \over \partial v}\parallel {\partial {\vec {x}} \over \partial v},\quad$ that means: the tangent vectors for fixed parameters are parallel.
• ${\vec {n}}_{d}(u,v)=\pm {\vec {n}}(u,v),\quad$ that means: the normal vectors for fixed parameters match direction.
• $S_{d}=(1+dS)^{-1}S,\quad$ where $S_{d}$ and $S$ are the shape operators for ${\vec {x}}_{d}$ and ${\vec {x}}$, respectively.

The principal curvatures are the eigenvalues of the shape operator, the principal curvature directions are its eigenvectors, the Gaussian curvature is its determinant, and the mean curvature is half its trace.

• $S_{d}^{-1}=S^{-1}+dI,\quad$ where $S_{d}^{-1}$ and $S^{-1}$ are the inverses of the shape operators for ${\vec {x}}_{d}$ and ${\vec {x}}$, respectively.

The principal radii of curvature are the eigenvalues of the inverse of the shape operator, the principal curvature directions are its eigenvectors, the reciprocal of the Gaussian curvature is its determinant, and the mean radius of curvature is half its trace.

Note the similarity to the geometric properties of parallel curves.

Generalizations

Parallel curves directly generalize to higher dimensions, including parallel surfaces in three dimensions, and, with a little more work, pipe surfaces. Terminology varies widely for higher dimensional generalizations since there are multiple kinds. Names include parallel fibers, ribbons, and tubes. For curves embedded in 3D surfaces the offset may be taken along a geodesic.

An envelope of ellipses forming two general offset curves above and below a generating curve

Another way to generalize parallel curves is, even in 2D, to consider a variable distance, for example, a situation where the distance is parameterized by another function. Other generalizations involve stroking, i.e. forming the envelope, with an ellipse instead of circle, as it is possible for example in METAFONT. In 2010, a similar feature was added in Adobe Illustrator in version CS5, where control points for the variable width are visually specified.

In contexts where it's important to distinguish between constant and variable distance offsetting the acronyms "CDO" for "constant distance offsetting" and "VDO" for "variable distance offsetting" are sometimes used.

General parallel curves

A regular parametric representation of a curve, ${\vec {x}}(t)=(x(t),y(t))$, together with a second function that can be parameterized by its unit normal, ${\vec {d}}({\vec {n}})$, where the normal of ${\vec {d}}({\vec {n}})={\vec {n}}$ . The parametric representation of the general offset curve of ${\vec {x}}(t)$ offset by ${\vec {d}}({\vec {n}})$ is:

${\vec {x}}_{d}(t)={\vec {x}}(t)+{\vec {d}}({\vec {n}}(t)),\quad$ where ${\vec {n}}(t)$ is the unit normal of ${\vec {x}}(t)$.

Note that the trivial offset, ${\vec {d}}({\vec {n}})=d{\vec {n}}$, gives you ordinary parallel (aka, offset) curves.

(this parameterization by normal exists for curves whose curvature is strictly positive or negative, and thus convex, smooth, and not straight)

Geometric properties

• The curvature of the a parallel curve, $k_{d}(t)$, the curvature of ${\vec {x}}(t)$, $k(t)$, and $k_{n}(t)$ the curvature of ${\vec {d}}({\vec {n}}(t))$ are related such that ${\textstyle k_{d}(t)={\dfrac {k(t)}{1+{\dfrac {k(t)}{k_{n}(t)}}}}.}$
• $R_{d}(t)=R(t)+R_{n}(t),\quad$ with $R_{d}(t)$ the radius of curvature of the general offset curve, $R(t)$ the radius of curvature of ${\vec {x}}(t)$, and $R_{n}(t)$ the radius of curvature of ${\vec {d}}({\vec {n}}(t))$ for parameter $t$.

General parallel surfaces

General parallel surfaces describe the shape of cuts made by a variety of cutting bits used by three-axis end mills in numerically controlled machining. Assume you have a regular parametric representation of a surface, ${\vec {x}}(u,v)=(x(u,v),y(u,v),z(u,v))$, and you have a second surface that can be parameterized by its unit normal, ${\vec {d}}({\vec {n}})$, where the normal of ${\vec {d}}({\vec {n}})={\vec {n}}$ (this parameterization by normal exists for surfaces whose Gaussian curvature is strictly positive, and thus convex, smooth, and not flat). The parametric representation of the general parallel surface of ${\vec {x}}(t)$ offset by ${\vec {d}}({\vec {n}})$ is:

${\vec {x}}_{d}(u,v)={\vec {x}}(u,v)+{\vec {d}}({\vec {n}}(u,v)),\quad$ where ${\vec {n}}(u,v)$ is the unit normal of ${\vec {x}}(u,v)$.

Note that the trivial offset, ${\vec {d}}({\vec {n}})=d{\vec {n}}$, gives you ordinary parallel (aka, offset) surfaces.

Geometric properties

• As for parallel lines, the tangent plane of a surface is parallel to the tangent plane of its general offsets.
• As for parallel lines, a normal to a surface is also normal to its general offsets.
• $S_{d}=(1+SS_{n}^{-1})^{-1}S,\quad$ where $S_{d},S,$ and $S_{n}$ are the shape operators for ${\vec {x}}_{d},{\vec {x}},$ and ${\vec {d}}({\vec {n}})$, respectively.

The principal curvatures are the eigenvalues of the shape operator, the principal curvature directions are its eigenvectors, the Gaussian curvature is its determinant, and the mean curvature is half its trace.

• $S_{d}^{-1}=S^{-1}+S_{n}^{-1},\quad$ where $S_{d}^{-1},S^{-1}$ and $S_{n}^{-1}$ are the inverses of the shape operators for ${\vec {x}}_{d},{\vec {x}},$ and ${\vec {d}}({\vec {n}})$, respectively.

The principal radii of curvature are the eigenvalues of the inverse of the shape operator, the principal curvature directions are its eigenvectors, the reciprocal of the Gaussian curvature is its determinant, and the mean radius of curvature is half its trace.

Note the similarity to the geometric properties of general offset curves.

Derivations of properties

The geometric properties listed above for general offset curves and surfaces can be derived for offsets of arbitrary dimension. Assume you have a regular parametric representation of an n-dimensional surface, ${\vec {x}}({\vec {u}})$, where the dimension of ${\vec {u}}$ is n-1. Also assume you have a second n-dimensional surface that can be parameterized by its unit normal, ${\vec {d}}({\vec {n}})$, where the normal of ${\vec {d}}({\vec {n}})={\vec {n}}$ (this parameterization by normal exists for surfaces whose Gaussian curvature is strictly positive, and thus convex, smooth, and not flat). The parametric representation of the general parallel surface of ${\vec {x}}({\vec {u}})$ offset by ${\vec {d}}({\vec {n}})$ is:

${\vec {x}}_{d}({\vec {u}})={\vec {x}}({\vec {u}})+{\vec {d}}({\vec {n}}({\vec {u}})),\quad$ where ${\vec {n}}({\vec {u}})$ is the unit normal of ${\vec {x}}({\vec {u}})$. (The trivial offset, ${\vec {d}}({\vec {n}})=d{\vec {n}}$, gives you ordinary parallel surfaces.)

First, notice that the normal of ${\vec {x}}({\vec {u}})=$ the normal of ${\vec {d}}({\vec {n}}({\vec {u}}))={\vec {n}}({\vec {u}}),$ by definition. Now, we'll apply the differential w.r.t. ${\vec {u}}$ to ${\vec {x}}_{d}$, which gives us its tangent vectors spanning its tangent plane.

$\partial {\vec {x}}_{d}({\vec {u}})=\partial {\vec {x}}({\vec {u}})+\partial {\vec {d}}({\vec {n}}({\vec {u}}))$

Notice, the tangent vectors for ${\vec {x}}_{d}$ are the sum of tangent vectors for ${\vec {x}}({\vec {u}})$ and its offset ${\vec {d}}({\vec {n}})$, which share the same unit normal. Thus, the general parallel surface shares the same tangent plane and normal with ${\vec {x}}({\vec {u}})$ and ${\vec {d}}({\vec {n}}({\vec {u}}))$. That aligns with the nature of envelopes.

We now consider the Weingarten equations for the shape operator, which can be written as $\partial {\vec {n}}=-\partial {\vec {x}}S$. If $S$ is invertible, $\partial {\vec {x}}=-\partial {\vec {n}}S^{-1}$. Recall that the principal curvatures of a surface are the eigenvalues of the shape operator, the principal curvature directions are its eigenvectors, the Gauss curvature is its determinant, and the mean curvature is half its trace. The inverse of the shape operator holds these same values for the radii of curvature.

Substituting into the equation for the differential of ${\vec {x}}_{d}$, we get:

$\partial {\vec {x}}_{d}=\partial {\vec {x}}-\partial {\vec {n}}S_{n}^{-1},\quad$ where $S_{n}$ is the shape operator for ${\vec {d}}({\vec {n}}({\vec {u}}))$.

Next, we use the Weingarten equations again to replace $\partial {\vec {n}}$:

$\partial {\vec {x}}_{d}=\partial {\vec {x}}+\partial {\vec {x}}SS_{n}^{-1},\quad$ where $S$ is the shape operator for ${\vec {x}}({\vec {u}})$.

Then, we solve for $\partial {\vec {x}}$ and multiple both sides by $-S$ to get back to the Weingarten equations, this time for $\partial {\vec {x}}_{d}$:

$\partial {\vec {x}}_{d}(I+SS_{n}^{-1})^{-1}=\partial {\vec {x}},$

$-\partial {\vec {x}}_{d}(I+SS_{n}^{-1})^{-1}S=-\partial {\vec {x}}S=\partial {\vec {n}}.$

Thus, $S_{d}=(I+SS_{n}^{-1})^{-1}S$, and inverting both sides gives us, $S_{d}^{-1}=S^{-1}+S_{n}^{-1}$.

See also

• Bump mapping
• Distance function and Signed distance function
• Distance field
• Offset printing
• Tubular neighborhood

References

• Josef Hoschek: Offset curves in the plane. In: CAD. 17 (1985), S. 77–81.
• Takashi Maekawa: An overview of offset curves and surfaces. In: CAD. 31 (1999), S. 165–173.

Further reading

• Farouki, R. T.; Neff, C. A. (1990). "Analytic properties of plane offset curves". Computer Aided Geometric Design. 7 (1–4): 83–99. doi:10.1016/0167-8396(90)90023-K.
• Piegl, Les A. (1999). "Computing offsets of NURBS curves and surfaces". Computer-Aided Design. 31 (2): 147–156. CiteSeerX 10.1.1.360.2793. doi:10.1016/S0010-4485(98)00066-9.
• Porteous, Ian R. (2001). Geometric Differentiation: For the Intelligence of Curves and Surfaces (2nd ed.). Cambridge University Press. pp. 1–25. ISBN 978-0-521-00264-6.
• Patrikalakis, Nicholas M.; Maekawa, Takashi (2010) [2002]. Shape Interrogation for Computer Aided Design and Manufacturing. Springer Science & Business Media. Chapter 11. Offset Curves and Surfaces. ISBN 978-3-642-04074-0. Free online version.
• Anton, François; Emiris, Ioannis Z.; Mourrain, Bernard; Teillaud, Monique (May 2005). "The O set to an Algebraic Curve and an Application to Conics". International Conference on Computational Science and its Applications. Singapore: Springer Verlag. pp. 683–696.
• Farouki, Rida T. (2008). Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable. Springer Science & Business Media. pp. 141–178. ISBN 978-3-540-73397-3. Pages listed are the general and introductory material.
• Au, C. K.; Ma, Y.-S. (2013). "Computation of Offset Curves Using a Distance Function: Addressing a Key Challenge in Cutting Tool Path Generation". In Ma, Y.-S. (ed.). Semantic Modeling and Interoperability in Product and Process Engineering: A Technology for Engineering Informatics. Springer Science & Business Media. pp. 259–273. ISBN 978-1-4471-5073-2.

External links

• Parallel curves on MathWorld
• Visual Dictionary of Plane Curves Xah Lee
• http://library.imageworks.com/pdfs/imageworks-library-offset-curve-deformation-from-Skeletal-Anima.pdf application to animation; patented as http://www.google.com/patents/US8400455

Category:Curves Category:Differential geometry Category:Articles containing video clips