User:TentativeTypist/sandbox

Derivative

The graph of an arbitrary function $y=f(x)$. The orange line is tangent to $x=a$, meaning at that exact point, the slope of the curve and the straight line are the same.

The derivative at different points of a differentiable function

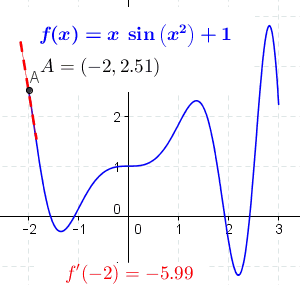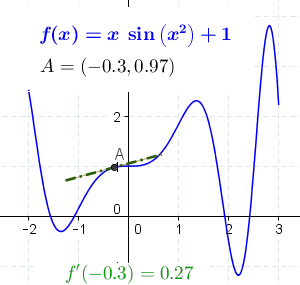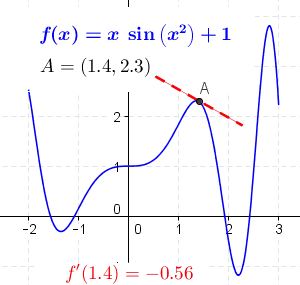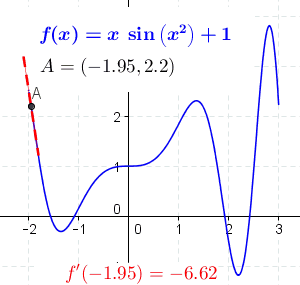
The derivative of $f(x)$ at the point $x=a$, denoted $f'(a)$, is defined as the slope of the tangent to $(a,f(a))$. In order to gain an intuition for this definition, one must first be familiar with finding the slope of a linear equation, written in the form $y=mx+b$. The slope of an equation is its steepness. It can be found by picking any two points and dividing the change in $y$ by the change in $x$, meaning that ${\text{slope }}={\tfrac {{\text{change in }}y}{{\text{change in }}x}}$. As an example, the graph of $y=-2x+13$ has a slope of $-2$, as shown in the diagram below:

The graph of $y=-2x-13$

${\frac {{\text{change in }}y}{{\text{change in }}x}}={\frac {-6}{+3}}=-2$

For brevity, ${\frac {{\text{change in }}y}{{\text{change in }}x}}$ is often written as ${\frac {\Delta y}{\Delta x}}$, with $\Delta$ being the Greek letter Delta, meaning 'change' or 'increment'. The slope of a linear equation is constant, meaning that the steepness is the same everywhere. However, many graphs, including $y=x^{2}$, vary in their steepness. This means that one can no longer pick any two arbitrary points and compute the slope. Instead, the slope of the graph is defined using a tangent line—a line that 'just touches' a particular point. The slope of a curve at a particular point is defined as the slope of the tangent to that point. For example, $y=x^{2}$ has a slope of $4$ at $x=2$, because the slope of the tangent line to that point is equal to $4$:

The graph of $y=x^{2}$, with a straight line that is tangent to $(2,4)$. The slope of the tangent line is equal to $4$. (Note that the axes of the graph do not use a 1:1 scale.)

The derivative of a function is defined as the slope of this tangent line. Even though the tangent line only touches a single point, it can be approximated by a line that goes through two points. This is known as a secant line. If the two points that the secant line goes through are close together, then the secant line closely resembles the tangent line, and, as a result, its slope is also very similar:

The dotted line goes through the points $(2,4)$ and $(3,9)$, which both lie on the curve $y=x^{2}$. Because these two points are fairly close together, the dotted line and tangent line have a similar slope. As the two points become closer together, the error produced by the secant line becomes vanishingly small.

The advantage of using a secant line is that its slope can be calculated directly. Consider the two points on the graph $(x,f(x))$ and $(x+\Delta x,f(x+\Delta x))$, where $\Delta x$ is a small number. As before, the slope of the line passing through these two points can be calculated with the formula ${\text{slope }}={\frac {\Delta y}{\Delta x}}$. This gives

${\text{slope}}={\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

As $\Delta x$ gets closer and closer to $0$, the slope of the secant line gets closer and closer to the slope of the tangent line. This is formally written as

$\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

The above expression means 'as $x$ gets closer and closer to 0, the slope of the secant line gets closer and closer to a certain value'. The value that is being approached is the derivative of $f(x)$; this can be written as $f'(x)$. If $y=f(x)$, the derivative can also be written as ${\tfrac {dy}{dx}}$, with $d$ representing an infinitesimal change. For example, $dx$ represents an infinitesimal change in x. In summary, if $y=f(x)$, then the derivative of $f(x)$ is

${\frac {dy}{dx}}=f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

provided such a limit exists. Differentiating a function using the above definition is known as differentiation from first principles. Here is a proof, using differentiation from first principles, that the derivative of $y=x^{2}$ is $2x$:

${\begin{aligned}{\frac {dy}{dx}}&=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {(x+\Delta x)^{2}-x^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {x^{2}+2x\Delta x+(\Delta x)^{2}-x^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {2x\Delta x+(\Delta x)^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}2x+\Delta x\\\end{aligned}}$

As $\Delta x\to 0$, $2x+\Delta x\to 2x$. Therefore, ${\tfrac {dy}{dx}}=2x$. This proof can be generalised to show that ${\tfrac {d(ax^{n})}{dx}}=anx^{n-1}$, if $a$ and $n$ are constants. This is known as the power rule. For example, ${\tfrac {d}{dx}}(5x^{4})=5(4)x^{3}=20x^{3}$. However, many other functions cannot be differentiated as easily as polynomial functions, meaning that sometimes further techniques are needed to find the derivative of a function. These techniques include the chain rule, product rule, and quotient rule. Other functions cannot be differentiated at all, giving rise to the concept of differentiability.

Derivative

The graph of an arbitrary function $y=f(x)$. The orange line is tangent to $x=a$, meaning at that exact point, the slope of the curve and the straight line are the same.

The derivative at different points of a differentiable function

The derivative of $f(x)$ at the point $x=a$, denoted $f'(a)$, is defined as the slope of the tangent to $(a,f(a))$. In order to gain an intuition for this definition, one must first be familiar with finding the slope of a linear equation, written in the form $y=mx+b$. The slope of an equation is its steepness. It can be found by picking any two points and dividing the change in $y$ by the change in $x$, meaning that ${\text{slope }}={\tfrac {{\text{change in }}y}{{\text{change in }}x}}$. As an example, the graph of $y=-2x+13$ has a slope of $-2$, as shown in the diagram below:

The graph of $y=-2x-13$

${\frac {{\text{change in }}y}{{\text{change in }}x}}={\frac {-6}{+3}}=-2$

For brevity, ${\frac {{\text{change in }}y}{{\text{change in }}x}}$ is often written as ${\frac {\Delta y}{\Delta x}}$, with $\Delta$ being the Greek letter Delta, meaning 'change' or 'increment'. The slope of a linear equation is constant, meaning that the steepness is the same everywhere. However, many graphs, including $y=x^{2}$, vary in their steepness. This means that one can no longer pick any two arbitrary points and compute the slope. Instead, the slope of the graph is defined using a tangent line—a line that 'just touches' a particular point. The slope of a curve at a particular point is defined as the slope of the tangent to that point. For example, $y=x^{2}$ has a slope of $4$ at $x=2$, because the slope of the tangent line to that point is equal to $4$:

The graph of $y=x^{2}$, with a straight line that is tangent to $(2,4)$. The slope of the tangent line is equal to $4$. (Note that the axes of the graph do not use a 1:1 scale.)

The derivative of a function is defined as the slope of this tangent line. Even though the tangent line only touches a single point, it can be approximated by a line that goes through two points. This is known as a secant line. If the two points that the secant line goes through are close together, then the secant line closely resembles the tangent line, and, as a result, its slope is also very similar:

The dotted line goes through the points $(2,4)$ and $(3,9)$, which both lie on the curve $y=x^{2}$. Because these two points are fairly close together, the dotted line and tangent line have a similar slope. As the two points become closer together, the error produced by the secant line becomes vanishingly small.

The advantage of using a secant line is that its slope can be calculated directly. Consider the two points on the graph $(x,f(x))$ and $(x+\Delta x,f(x+\Delta x))$, where $\Delta x$ is a small number. As before, the slope of the line passing through these two points can be calculated with the formula ${\text{slope }}={\frac {\Delta y}{\Delta x}}$. This gives

${\text{slope}}={\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

As $\Delta x$ gets closer and closer to $0$, the slope of the secant line gets closer and closer to the slope of the tangent line. This is formally written as

$\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

The above expression means 'as $x$ gets closer and closer to 0, the slope of the secant line gets closer and closer to a certain value'. The value that is being approached is the derivative of $f(x)$; this can be written as $f'(x)$. If $y=f(x)$, the derivative can also be written as ${\tfrac {dy}{dx}}$, with $d$ representing an infinitesimal change. For example, $dx$ represents an infinitesimal change in x. In summary, if $y=f(x)$, then the derivative of $f(x)$ is

${\frac {dy}{dx}}=f'(x)=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

provided such a limit exists. Differentiating a function using the above definition is known as differentiation from first principles. Here is a proof, using differentiation from first principles, that the derivative of $y=x^{2}$ is $2x$:

${\begin{aligned}{\frac {dy}{dx}}&=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {(x+\Delta x)^{2}-x^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {x^{2}+2x\Delta x+(\Delta x)^{2}-x^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {2x\Delta x+(\Delta x)^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}2x+\Delta x\\\end{aligned}}$

As $\Delta x\to 0$, $2x+\Delta x\to 2x$. Therefore, ${\tfrac {dy}{dx}}=2x$. This proof can be generalised to show that ${\tfrac {d(ax^{n})}{dx}}=anx^{n-1}$, if $a$ and $n$ are constants. This is known as the power rule. For example, ${\tfrac {d}{dx}}(5x^{4})=5(4)x^{3}=20x^{3}$. However, many other functions cannot be differentiated as easily as polynomial functions, meaning that sometimes further techniques are needed to find the derivative of a function. These techniques include the chain rule, product rule, and quotient rule. Other functions cannot be differentiated at all, giving rise to the concept of differentiability.

Exponentiation

Defining exponentiation via logarithms

The meaning of $a^{x}$, where $a$ and $x$ are positive real numbers, can also come from natural logarithm. This avoids the difficulty surrounding the definition of $a^{x}$ for irrational $x$. First, we may define, for $x>0$,

$\log x=\int _{1}^{x}{\frac {1}{t}}dt$

It can then be proven that $\log x$ satisfies the basic properties of logarithms, in particular $\log a+\log b=\log ab$. Then, $\exp$ can be defined as the inverse of $\log$, and $e$ can be defined as the number $a$ such that $\log a=1$.

$e$ is the unique number such that the shaded region has an area of $1$. This region is bounded by the $x$-axis, the vertical lines $x=1$ and $x=e$, and the hyperbola $y=1/x$.

Finally, $a^{x}$ can be defined as $\exp(x\log a)$. Since $e^{x}=\exp(x\log e)=\exp(x)$, $a^{x}$ can also be interpreted to mean $e^{x\log a}$. In any case, this approach sidesteps the issue surrounding the definition of $a^{x}$ for irrational $x$; in fact, $a^{x}$ has the same definition regardless of whether $x$ is a natural number, an integer, a rational number, or a real number.

Small-angle approximation

Algebraic

The small-angle approximation for the sine function.

The Maclaurin series expansions of the main trigonometric functions are

${\begin{aligned}\sin \theta &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}\theta ^{2n+1}\\&=\theta -{\frac {\theta ^{3}}{3!}}+{\frac {\theta ^{5}}{5!}}-{\frac {\theta ^{7}}{7!}}+\cdots \\[6pt]\cos \theta &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}\theta ^{2n}\\&=1-{\frac {\theta ^{2}}{2!}}+{\frac {\theta ^{4}}{4!}}-{\frac {\theta ^{6}}{6!}}+\cdots \theta \\[6pt]\tan \theta &=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}\theta ^{2n-1}\\&=\theta +{\frac {\theta ^{3}}{3}}+{\frac {2\theta ^{5}}{15}}+{\frac {17\theta ^{7}}{315}}+\cdots \\[6pt]\end{aligned}}$

where θ is the angle in radians.

It is readily seen that the second most significant (third-order) term falls off as the cube of the first term; thus, even for a not-so-small argument such as 0.01, the value of the second most significant term is on the order of 0.000001, or 1/10000 the first term. One can thus safely approximate:

$\sin \theta \approx \theta$

By extension, since the cosine of a small angle is very nearly 1, and the tangent is given by the sine divided by the cosine,

$\tan \theta \approx \sin \theta \approx \theta$,

Overview

Unlike factoring by inspection, completing the square can be used to solve any quadratic equation. Consider the example

$x^{2}+10x=39\,.$

In order to isolate for $x$, it helps to consider this problem geometrically. The first term, $x^{2}$ can be interpreted as the area of square with side length $x$. The second term, $10x$ can be interpreted as the area of a rectangle with lengths $10$ and $x$, or, as the combined area of two rectangles that have lengths $5$ and $x$:

This diagram suggests that $x^{2}+10x$ is almost a perfect square with side length $x+5$. If we add $25$ to both sides of the equation, then it becomes

$x^{2}+10x+25=64$

The left-hand side of the equation can then be written as $(x+5)^{2}$, and so

$(x+5)^{2}=64$