User:Phlsph7/Algebra - Elementary algebra

Elementary algebra

Main article: Elementary algebra

Algebraic expression notation:
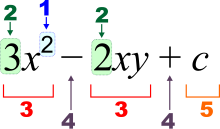
  1 – power (exponent)
  2 – coefficient
  3 – term
  4 – operator
  5 – constant term
  x y c – variables/constants

Elementary algebra, also referred to as school algebra and classical algebra, is the oldest and most basic form of algebra. It is a generalization of arithmetic that relies on the use of variables and examines how formulas may be transformed. Arithmetic is the study of numerical operations and investigates how numbers are combined and transformed using arithmetic operations like addition, subtraction, multiplication, and division. For example, the operation of addition combines two numbers, called the addends, into a third number, called the sum, as in $2+5=7$. Elementary algebra uses the same operations while allowing the use of variables in addition to regular numbers. This makes it possible to state general laws that are true independent of which numbers are used. For example, the equation $2\times 3=3\times 2$ belongs to arithmetic and expresses an equality only for these specific numbers. By replacing the numbers with variables, it is possible to express a general law that applies to any possible combinations of numbers, as in the equation $a\times b=b\times a$.

Elementary algebra is interested in algebraic expressions, which are formed by using arithmetic operations to combine variables and numbers. For example, the expression $5x+3$ is an algebraic expression created by multiplying the number 5 with the variable x and adding the number 3 to the result. Other examples of algebraic equations are $32xyz$ and $64x^{2}+7y-13$.

Algebraic expressions are used to construct statements that relate two expressions to one another. An equation is a statement formed by comparing two expressions using an equals sign (=), as in $5x^{2}+6x=3y+4$. Inequations are formed using symbols like the less-than sign (<) and the greater-than sign (>). Unlike mere expressions, statements can be true or false and their truth value usually depends on the values of the variables. For example, the statement $x^{2}=4$ is true if x is either 2 or -2 and false otherwise.

The main objective of elementary algebra is to determine for which values a statement is true. To achieve this, it relies on different techniques used to transform and manipulate statements. A key principle guiding this process is that whatever is done to one side of an equation also needs to be done to the other side of the equation. For example, if one subtracts 5 from the left side of an equation one also needs to subtract 5 from the right side of the equation to balance both sides. The goal of these steps is usually to isolate the variable one is interested in on one side, a process known as solving the equation for that variable. For example, the equation $x-7=4$ can be solved for x by adding 7 to both sides, which isolates x on the left side and results in the equation $x=11$.

There are many other techniques used to solve equations. Simplification is used to replace a complicated expression with an equivalent simpler one. For example, the expression $7x-3x$ can be replaced with the expression $4x$. Factorization is used to rewrite an expression as a product of several factors. This technique is common for polynomials to determine for which values the expression is zero. For example, the polynomial $x^{2}-3x-10$ can be factorized as $(x+2)(x-5)$. The polynomial as a whole is zero if one of its factors is zero, i.e., if x is either -2 or 5. For statements using several variables, substitution is a common technique to replace one variable with an equivalent expression that does not use this variable. For example, if one knows that $y=3x$ then one can simplify the expression $7xy$ to arrive at $21x^{2}$. Other techniques include making use of the commutative, distributive, and associative properties.

Algebraic equations can be used to describe geometric figures. All values for x and y that solve the equation are interpreted as points and drawn as a red line.

Elementary algebra has applications in many branches of mathematics, the sciences, business, and everyday life. An important application in the field of geometry concerns the use of algebraic equations to describe geometric figures in the form of a graph. To do so, the different variables in the equation are interpreted as coordinates and the values that solve the equation are interpreted as points of the graph. For example, if x is set to zero in the equation $y=0.5x-1$ then y has to be -1 for the equation to be true. This means that the x-y-pair (0, -1) is part of the graph of the equation. The x-y-pair (0, 7), by contrast, does not solve the equation and is therefore not part of the graph. The graph encompasses the totality of all x-y-pairs that solve the equation.

References

• Benson, Donald C. (2003). A Smoother Pebble: Mathematical Explorations. Oxford University Press. ISBN 978-0-19-514436-9.
• Rohde, Ulrich L.; Jain, G. C.; Poddar, Ajay K.; Ghosh, A. K. (12 January 2012). Introduction to Differential Calculus: Systematic Studies with Engineering Applications for Beginners. John Wiley & Sons. ISBN 978-1-118-13014-8.
• Axler, Sheldon (8 March 2011). Algebra and Trigonometry. John Wiley & Sons. ISBN 978-0-470-58579-5.
• McKeague, Charles P. (10 May 2014). Intermediate Algebra: A Text/Workbook. Academic Press. ISBN 978-1-4832-1417-7.
• Zill, Dennis; Dewar, Jacqueline (19 January 2011). Algebra and Trigonometry. Jones & Bartlett Publishers. ISBN 978-0-7637-5461-7.
• Lamagna, Edmund A. (15 January 2019). Computer Algebra: Concepts and Techniques. CRC Press. ISBN 978-1-351-60583-0.
• Berggren, John L. (2015). "Elementary algebra". Encyclopædia Britannica. Retrieved 14 January 2024.
• Buthusiem, Gregory; Toth, Gabor (2020). Precalculus. Linus Learning. ISBN 978-1-60797-798-8.
• Young, Cynthia Y. (19 January 2010). Precalculus. John Wiley & Sons. ISBN 978-0-471-75684-2.
• Majewski, Miroslaw (2004). MuPAD Pro computing essentials (2 ed.). Berlin Heidelberg New York: Springer. ISBN 978-3-540-21943-9.
• Tan, Kiat Shi; Steeb, Willi-Hans; Hardy, Yorick (6 December 2012). SymbolicC++:An Introduction to Computer Algebra using Object-Oriented Programming: An Introduction to Computer Algebra using Object-Oriented Programming. Springer Science & Business Media. ISBN 978-1-4471-0405-6.