User:Patrick/regular polyhedron

Platonic solids

Combinatorial properties

A convex polyhedron is a Platonic solid if and only if

1. all its faces are congruent convex regular polygons,
2. none of its faces intersect except at their edges, and
3. the same number of faces meet at each of its vertices.

Each Platonic solid can therefore be denoted by a symbol {p, q} where

p is the number of edges (or, equivalently, vertices) of each face, and

q is the number of faces (or, equivalently, edges) that meet at each vertex.

The symbol {p, q}, called the Schläfli symbol, gives a combinatorial description of the polyhedron. The Schläfli symbols of the five Platonic solids are given in the table below.

Polyhedron		Vertices	Edges	Faces	Schläfli symbol	Vertex configuration
tetrahedron		4	6	4	{3, 3}	3.3.3
cube		8	12	6	{4, 3}	4.4.4
octahedron		6	12	8	{3, 4}	3.3.3.3
dodecahedron		20	30	12	{5, 3}	5.5.5
icosahedron		12	30	20	{3, 5}	3.3.3.3.3

All other combinatorial information about these solids, such as total number of vertices (V), edges (E), and faces (F), can be determined from p and q. Since any edge joins two vertices and has two adjacent faces we must have:

$pF=2E=qV.\,$

The other relationship between these values is given by Euler's formula:

$V-E+F=2.\,$

This can be proved in many ways. Together these three relationships completely determine V, E, and F:

$V={\frac {4p}{4-(p-2)(q-2)}},\quad E={\frac {2pq}{4-(p-2)(q-2)}},\quad F={\frac {4q}{4-(p-2)(q-2)}}.$

$V={\frac {4p}{2p+2q-pq}},\quad E={\frac {2pq}{2p+2q-pq}},\quad F={\frac {4q}{2p+2q-pq}}.$

$E={\frac {1}{{\frac {1}{p}}+{\frac {1}{q}}-{\frac {1}{2}}}},\quad V={\frac {2E}{q}},\quad F={\frac {2E}{p}}.$

$E={\frac {2pq}{4-(p-2)(q-2)}},\quad V={\frac {2E}{q}},\quad F={\frac {2E}{p}}.$

Swapping p and q interchanges F and V while leaving E unchanged.

Symmetry groups

In mathematics, the concept of symmetry is studied with the notion of a mathematical group. Every polyhedron has an associated symmetry group, which is the set of all transformations (Euclidean isometries) which leave the polyhedron invariant. The order of the symmetry group is the number of symmetries of the polyhedron. One often distinguishes between the full symmetry group, which includes reflections, and the proper symmetry group, which includes only rotations.

The symmetry groups of the Platonic solids are a special class of three-dimensional point groups known as polyhedral groups. The high degree of symmetry of the Platonic solids can be interpreted in a number of ways. Most importantly, the vertices of each solid are all equivalent under the action of the symmetry group, as are the edges and faces. One says the action of the symmetry group is transitive on the vertices, edges, and faces. In fact, this is another way of defining regularity of a polyhedron: a polyhedron is regular if and only if it is vertex-uniform, edge-uniform, and face-uniform.

There are only three symmetry groups associated with the Platonic solids rather than five, since the symmetry group of any polyhedron coincides with that of its dual. This is easily seen by examining the construction of the dual polyhedron. Any symmetry of the original must be a symmetry of the dual and vice versa. The three polyhedral groups are:

• the tetrahedral group T,
• the octahedral group O (which is also the symmetry group of the cube), and
• the icosahedral group I (which is also the symmetry group of the dodecahedron).

The orders of the proper (rotation) groups are 12, 24, and 60 respectively – precisely twice the number of edges in the respective polyhedra. The orders of the full symmetry groups are twice as much again (24, 48, and 120). See (Coxeter 1973) for a derivation of these facts. All Platonic solids except the tetrahedron are centrally symmetric, meaning they are preserved under reflection through the origin.

The following table lists the various symmetry properties of the Platonic solids. The symmetry groups listed are the full groups with the rotation subgroups given in parenthesis (likewise for the number of symmetries). Wythoff's kaleidoscope construction is a method for constructing polyhedra directly from their symmetry groups. They are listed for reference Wythoff's symbol for each of the Platonic solids.

Polyhedron	Schläfli symbol	Wythoff symbol	Dual polyhedron	Symmetry group (Reflection, rotation)
				Polyhedral	Schön.	Cox.	Orb.	Order
tetrahedron	{3, 3}	3 | 2 3	tetrahedron	Tetrahedral	Td T	[3,3] [3,3]+	*332 332	24 12
cube	{4, 3}	3 | 2 4	octahedron	Octahedral	Oh O	[4,3] [4,3]+	*432 432	48 24
octahedron	{3, 4}	4 | 2 3	cube
dodecahedron	{5, 3}	3 | 2 5	icosahedron	Icosahedral	Ih I	[5,3] [5,3]+	*532 532	120 60
icosahedron	{3, 5}	5 | 2 3	dodecahedron

Regular tessellations

The three regular tessellations of the plane are closely related to the Platonic solids. Indeed, one can view the Platonic solids as regular tessellations of the sphere. Every regular tessellation of the sphere is characterized by a pair of integers {p, q} with 1/p + 1/q > 1/2. Likewise, a regular tessellation of the plane is characterized by the condition 1/p + 1/q = 1/2. There are three possibilities:

The three regular tilings of the Euclidean plane

{4, 4}	{3, 6}	{6, 3}

Star polyhedron

The four Kepler–Poinsot polyhedra are illustrated above. Each is identified by its Schläfli symbol, of the form {p, q}, and by its name. One face of each figure is shown yellow and outlined in red.

In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.

They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures.

Characteristics

Non-convexity

These figures have pentagrams (star pentagons) as faces or vertex figures. The small and great stellated dodecahedron have nonconvex regular pentagram faces. The great dodecahedron and great icosahedron have convex polygonal faces, but pentagrammic vertex figures.

In all cases, two faces can intersect along a line that is not an edge of either face, so that part of each face passes through the interior of the figure. Such lines of intersection are not part of the polyhedral structure and are sometimes called false edges. Likewise where three such lines intersect at a point that is not a corner of any face, these points are false vertices. The images below show golden balls at the true vertices, and silver rods along the true edges.

For example, the small stellated dodecahedron has 12 pentagram faces with the central pentagonal part hidden inside the solid. The visible parts of each face comprise five isosceles triangles which touch at five points around the pentagon. We could treat these triangles as 60 separate faces to obtain a new, irregular polyhedron which looks outwardly identical. Each edge would now be divided into three shorter edges (of two different kinds), and the 20 false vertices would become true ones, so that we have a total of 32 vertices (again of two kinds). The hidden inner pentagons are no longer part of the polyhedral surface, and can disappear. Now the Euler's formula holds: 60 − 90 + 32 = 2. However this polyhedron is no longer the one described by the Schläfli symbol {5/2, 5}, and so can not be a Kepler–Poinsot solid even though it still looks like one from outside.

Euler characteristic χ

A Kepler–Poinsot polyhedron covers its circumscribed sphere more than once, with the centers of faces acting as winding points in the figures which have pentagrammic faces, and the vertices in the others. Because of this, they are not necessarily topologically equivalent to the sphere as Platonic solids are, and in particular the Euler relation

$\chi =V-E+F=2\$

does not always hold. Schläfli held that all polyhedra must have χ = 2, and he rejected the small stellated dodecahedron and great dodecahedron as proper polyhedra. This view was never widely held.

A modified form of Euler's formula, using density (D) of the vertex figures ($d_{v}$) and faces ($d_{f}$) was given by Arthur Cayley, and holds both for convex polyhedra (where the correction factors are all 1), and the Kepler–Poinsot polyhedra:

$d_{v}V-E+d_{f}F=2D.$

Duality

The Kepler–Poinsot polyhedra exist in dual pairs:

• Small stellated dodecahedron and great dodecahedron and
• Great stellated dodecahedron and great icosahedron.

Summary

Name	Picture	Spherical tiling	Stellation diagram	Schläfli {p,q} and Coxeter-Dynkin	Faces {p}	Edges	Vertices {q}	Vertex figure (config.)	χ	Density	Symmetry	Dual
Small stellated dodecahedron (sissid)				{5/2,5}	12 {5/2}	30	12 {5}	(5/2)5	-6	3	Ih	Great dodecahedron
Great stellated dodecahedron (gissid)				{5/2,3}	12 {5/2}	30	20 {3}	(5/2)3	2	7	Ih	Great icosahedron
Great dodecahedron (gad)				{5,5/2}	12 {5}	30	12 {5/2}	(55)/2	-6	3	Ih	Small stellated dodecahedron
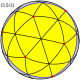
Great icosahedron (gike)				{3,5/2}	20 {3}	30	12 {5/2}	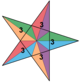(35)/2	2	7	Ih	Great stellated dodecahedron

Polyhedron compound

From Uniform polyhedron compound:

A uniform polyhedron compound is a polyhedral compound whose constituents are identical (although possibly enantiomorphous) uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.

The uniform polyhedron compounds were first enumerated by John Skilling in 1976, with a proof that the enumeration is complete. The following table lists them according to his numbering.

Compound	Bowers acronym	Picture	Polyhedral count	Polyhedral type	Faces	Edges	Vertices	Notes	Symmetry group	Subgroup restricting to one constituent
UC04	so		2	tetrahedra	8{3}	12	8	regular	Oh	Td
UC05	ki		5	tetrahedra	20{3}	30	20	regular	I	T
UC06	e		10	tetrahedra	40{3}	60	20	regular 2 constituent polyhedra incident on each vertex	Ih	T
UC09	rhom		5	cubes	30{4}	60	20	regular 2 constituent polyhedra incident on each vertex	Ih	Th
UC17	se		5	octahedra	40{3}	60	30	regular	Ih	Th

Relationships among the regular polyhedra

These share the same vertex arrangements:	These share the same vertex and edge arrangements:
The icosahedron, small stellated dodecahedron, great icosahedron, and great dodecahedron.	The small stellated dodecahedron and great icosahedron.
The dodecahedron and great stellated dodecahedron.	The icosahedron and great dodecahedron.

The small stellated dodecahedron and great icosahedron share the same vertices and edges. The icosahedron and great dodecahedron also share the same vertices and edges.

The three dodecahedra are all stellations of the regular convex dodecahedron, and the great icosahedron is a stellation of the regular convex icosahedron. The small stellated dodecahedron and the great icosahedron are facettings of the convex dodecahedron, while the two great dodecahedra are facettings of the regular convex icosahedron.

If the intersections are treated as new edges and vertices, the figures obtained will not be regular, but they can still be considered stellations. (See also List of Wenninger polyhedron models)