User:Menghuan007/sandbox

Image Rectification in Computer Vision

the search space before (1) and after (2) rectification

Introduction

We assume that a pair of 2D images of a 3D object or environment are taken from two distinct viewpoints and their epipolar geometry has been determined. Corresponding points between the two images must satisfy the so-called epipolar constraint. For a given point in one image, we have to search for its correspondence in the other image along an epipolar line. In general, epipolar lines are not aligned with coordinate axis and are not parallel. Such searches are time consuming since we must compare pixels on skew lines in image space. By applying 2D projective transforms or homographies, the epipolar lines can be axis aligned and parallel, so that the search can be more efficient. This process is known as image rectification.

Basic Idea

Stereo vision uses triangulation based on epipolar geometry to determine distance to an object. More specifically, binocular disparity is the process of relating the depth of an object to its change in position when viewed from a different camera, given the relative position of each camera is known.

With multiple cameras it can be difficult to find a corresponding point viewed by one camera in the image of the other camera (known as the correspondence problem). In most camera configurations, finding correspondences requires a search in two-dimensions. However, if the two cameras are aligned correctly to be coplanar, the search is simplified to one dimension - a horizontal line parallel to the line between the cameras. Furthermore, if the location of a point in the left image is known, it can be searched for in the right image by searching left of this location along the line, and vice versa (see binocular disparity). Image rectification is an equivalent (and more often used) alternative to perfect camera alignment. Even with high-precision equipment, image rectification is usually performed because it may be impractical to maintain perfect alignment between cameras.

Transformation

Epipolar geometry for a pair of cameras is implicit in the relative pose and calibrations of the cameras. The followings are some basic idea of epipolar geometry:

• Epipole is the point of intersection of the line joining the camera centers (the baseline) with the image plane. e0 and e1 in the figure.
• Epipolar plane is a plane containing the baseline. There is a one-parameter family (a pencil) of epipolar planes. The plane constructed by the camera c0, c1, and the point p is epipolar plane in the figure.
• Epipolar line is the intersection of an epipolar plane with the image plane. All epipolar lines intersect at the epipole. An epipolar plane intersects the left and right image planes in epipolar lines, and defines the correspondence between the lines.

The figure illustrate a pixel, on the line l0 of image x0, projects to epipolar line segment in the other image x1. The segment is bounded at one end by the projection of the original viewing ray at infinity p. The other end is bounded by the projection of the original camera center c0 into the second camera c1, which is known as the epipole e1. The transformation of two points can easily be computed from seven or more point matches using the fundamental matrix. If camera calibration is known, that is, an essential matrix provides the relationship between the cameras, only five or more points are needed to compute the fundamental matrix. The fundamental matrix is the algebraic representation of epipolar geometry and defined by $X'^{T}FX=0$. $X$ and $X'$ are pair points, and F is the fundamental matrix. The fundamental matrix can be solved by eight-point algorithm.

If the images to be rectified are taken from camera pairs without geometric distortion, this calculation can easily be made with a linear transformation. X & Y rotation puts the images on the same plane, scaling makes the image frames be the same size and Z rotation & skew adjustments make the image pixel rows directly line up. The rigid alignment of the cameras needs to be known (by calibration) and the calibration coefficients are used by the transform.

In performing the transform, if the cameras themselves are calibrated for internal parameters, an essential matrix provides the relationship between the cameras. The more general case (without camera calibration) is represented by the fundamental matrix. If the fundamental matrix is not known, it is necessary to find preliminary point correspondences between stereo images to facilitate its extraction.

Algorithms

There are three main categories for image rectification algorithms: planar rectification, cylindrical rectification and polar rectification. The different methods for rectification mainly differ in how the remaining degrees of freedom are chosen.

Planar rectification

The idea of planar rectification is to get ideal configuration by a transformation. This means, for each pixel on original image, a new pixel on rectified image is specified. It is accomplished by collinear condition for the old pixel and the new pixel. The planar rectification approach consists of selecting a plane parallel with the baseline. The two image are then re-projected into this plane. These new images satisfy the standard stereo setup. In the calibrated case, one can choose the distance from the plane to the baseline, so that no pixels are compressed during the warping from the images to the rectified images and the normal on the plane can be chosen in the middle of the two epipolar planes containing the optical axes.

Cylindrical rectification

The goal of cylindrical rectification is to apply a transformation of an original image to remap on the surface of a carefully selected cylinder instead of a plane. The transformation from image to cylinder is performed in three stages. First, a rotation is applied to a selected epipolar line. This rotation is in the epipolar plane and makes the epipolarline parallel to the foe. Then, a change of coordinate system is applied to the rotated epipolar line from the image system to the cylinder system (with foe as principal axis). Finally, this line is normalized or reprojected onto the surface of a cylinder of unit diameter. Since the line is already parallel to the cylinder, it is simply scaled along the direction perpendicular to the axis until it lies at unit distance from the axis.

Polar rectification

File:Polar rectification.png

Polar rectification

The idea of polar rectification is to transform each epipolar line on original image from pixel coordinate to polar coordinate, then put each epipolar line on rectified image sequentially. The process could be seen in Figure.

Implementation Details and Example

All rectified images satisfy the following two properties:

• All epipolar lines are parallel to the horizontal axis.
• Corresponding points have identical vertical coordinates.

In order to transform the original image pair into a rectified image pair, it is necessary to find a projective transformation H. Constraints are placed on H to satisfy the two properties above. For example, constraining the epipolar lines to be parallel with the horizontal axis means that epipoles must be mapped to the infinite point [1,0,0]^T in homogeneous coordinates. Even with these constraints, H still has four degrees of freedom. It is also necessary to find a matching H' to rectify the second image of an image pair. Poor choices of H and H' can result in rectified images that are dramatically changed in scale or severely distorted.

There are many different strategies for choosing a projective transform H for each image from all possible solutions. One advanced method is minimizing the disparity or least-square difference of corresponding points on the horizontal axis of the rectified image pair. Another method is separating H into a specialized projective transform, similarity transform, and shearing transform to minimize image distortion. One simple method is to rotate both images to look perpendicular to the line joining their collective optical centers, twist the optical axes so the horizontal axis of each image points in the direction of the other image's optical center, and finally scale the smaller image to match for line-to-line correspondence. This process is demonstrated in the following example.

Model used for image rectification example. (image source Silvio Savarese)

3D view of example scene. The first camera's optical center and image plane are represented by the green circle and square respectively. The second camera has similar red representations.

Set of 2D images from example. The original images are taken from different perspectives (row 1). Using systematic transformations from the example (rows 2 and 3), we are able to transform both images such that corresponding points are on the same horizontal scan lines (row 4).

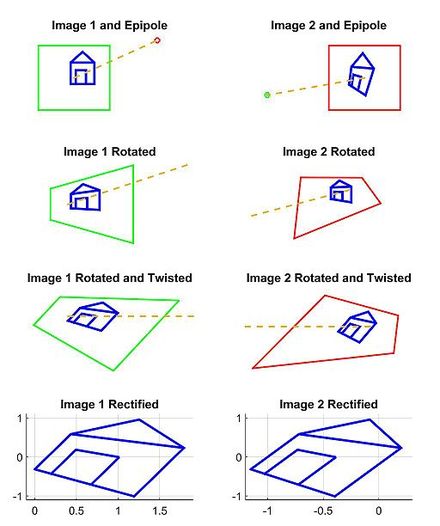
Our model for this example is based on a pair of images that observe a 3D point P, which corresponds to p and p' in the pixel coordinates of each image. O and O' represent the optical centers of each camera, with known camera matrices $M=K[I~0]$ and $M'=K'[R~T]$ (we assume the world origin is at the first camera). We will briefly outline and depict the results for a simple approach to find a H and H' projective transformation that rectify the image pair from the example scene.

First, we compute the epipoles, e and e' in each image:

$e=M{\begin{bmatrix}O'\\1\end{bmatrix}}=M{\begin{bmatrix}-R^{T}T\\1\end{bmatrix}}=K[I~0]{\begin{bmatrix}-R^{T}T\\1\end{bmatrix}}=-KR^{T}T$

$e'=M'{\begin{bmatrix}O\\1\end{bmatrix}}=M'{\begin{bmatrix}0\\1\end{bmatrix}}=K'[R~T]{\begin{bmatrix}0\\1\end{bmatrix}}=K'T$

Second, we find a projective transformation H₁ that rotates our first image to be perpendicular to the baseline connecting O and O' (row 2, column 1 of 2D image set). This rotation can be found by using the cross product between the original and the desired optical axes. Next, we find the projective transformation H₂ that takes the rotated image and twists it so that the horizontal axis aligns with the baseline. If calculated correctly, this second transformation should map the e to infinity on the x axis (row 3, column 1 of 2D image set). Finally, define $H=H_{2}H_{1}$ as the projective transformation for rectifying the first image.

Third, through an equivalent operation, we can find H' to rectify the second image (column 2 of 2D image set). Note that H'₁ should rotate the second image's optical axis to be parallel with the transformed optical axis of the first image. One strategy is to pick a plane parallel to the line where the two original optical axes intersect to minimize distortion from the reprojection process. In this example, we simply define H' using the rotation matrix R and initial projective transformation H as $H'=HR^{T}$.

Finally, we scale both images to the same approximate resolution and align the now horizontal epipoles for easier horizontal scanning for correspondences (row 4 of 2D image set).

Note that it is possible to perform this and similar algorithms without having the camera parameter matrices M and M' . All that is required is a set of seven or more image to image correspondences to compute the fundamental matrices and epipoles.

Goals of Image Rectification

The result of rectification is so called standard rectified geometry. It leads to a very simple inverse relationship between 3D depths Z and disparities d.

Depth computing: O1 and O2 are cameras, and X is the point

$d=f{\frac {B}{Z}}$

where f is the focal length (measured in pixels), B is the baseline, and

$x_{1}'=x_{2}'+d(x,y),y_{1}'=y_{2}'$

describes the relationship between corresponding pixel coordinates in the left and right images.

After rectification, the search for matching points is vastly simplified by the simple epipolar structure and by the near-correspondence of the two images. To discover corresponding point P in left and right images, we can firstly rectify two images. Pick up a window around P and build its feature vector w. Slide the window along the epipolar line in the other image. Compute the feature $w'$ when sliding the window. Find out the maximum $ww'$ and the corresponding $P'$ is the looking for point.

References

13. R. I. Hartley (1999). "Theory and Practice of Projective Rectification". Int. Journal of Computer Vision. 35 (2): 115–127. doi:10.1023/A:1008115206617.
14. Pollefeys, Marc. "Polar rectification". Retrieved 2007-06-09.
15. Linda G. Shapiro and George C. Stockman (2001). Computer Vision. Prentice Hall. p. 580. ISBN 0-13-030796-3.