User:Bensculfor/Mathematics history
The following is a draft rewrite of the history section of the article mathematics.
To-do list:
- Mayan mathematics (a paragraph in post-classical and medieval)
- Applied maths in the 19th century (Kovalevskaya, Maxwell, populations)
- Discrete maths in the twentieth century (graph theory, Ramsey theory, Erdős)
- Analysis in the twentieth century (functional analysis, harmonic analysis, dynamical systems)
- Applied maths in the twentieth century (optimisation, linear/nonlinear programming)
- ADD REFERENCES.
History[edit]
The history of mathematics can be seen as an ever-increasing series of abstractions. The first abstraction, which is shared by many animals,[1] was probably that of numbers: the realization that a collection of two apples and a collection of two oranges (for example) have something in common, namely quantity of their members.
Etymology[edit]
The word mathematics comes from Ancient Greek μάθημα (máthēma), meaning "that which is learnt",[2] "what one gets to know", hence also "study" and "science". The word for "mathematics" came to have the narrower and more technical meaning "mathematical study" even in Classical times.[3] Its adjective is μαθηματικός (mathēmatikós), meaning "related to learning" or "studious", which likewise further came to mean "mathematical". In particular, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), Latin: ars mathematica, meant "the mathematical art".
Similarly, one of the two main schools of thought in Pythagoreanism was known as the mathēmatikoi (μαθηματικοί)—which at the time meant "teachers" rather than "mathematicians" in the modern sense.
In Latin, and in English until around 1700, the term mathematics more commonly meant "astrology" (or sometimes "astronomy") rather than "mathematics"; the meaning gradually changed to its present one from about 1500 to 1800. This has resulted in several mistranslations. For example, Saint Augustine's warning that Christians should beware of mathematici, meaning astrologers, is sometimes mistranslated as a condemnation of mathematicians.[4]
The apparent plural form in English, like the French plural form les mathématiques (and the less commonly used singular derivative la mathématique), goes back to the Latin neuter plural mathematica (Cicero), based on the Greek plural τὰ μαθηματικά (ta mathēmatiká), used by Aristotle (384–322 BC), and meaning roughly "all things mathematical"; although it is plausible that English borrowed only the adjective mathematic(al) and formed the noun mathematics anew, after the pattern of physics and metaphysics, which were inherited from Greek.[5] In English, the noun mathematics takes a singular verb. It is often shortened to maths or, in North America, math.[6]
Prehistory[edit]
As evidenced by tallies found on bone, in addition to recognizing how to count physical objects, prehistoric peoples may have also recognized how to count abstract quantities, like time – days, seasons, years.[7]
Ancient History[edit]



Evidence for more complex mathematics does not appear until around 3000 BC, when the Babylonians and Egyptians began using arithmetic, algebra and geometry for taxation and other financial calculations, for building and construction, and for astronomy.[8] The most ancient mathematical texts from Mesopotamia and Egypt are from 2000–1800 BC. Many early texts mention Pythagorean triples and so, by inference, the Pythagorean theorem seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry. It is in Babylonian mathematics that elementary arithmetic (addition, subtraction, multiplication and division) first appear in the archaeological record. The Babylonians also possessed a place-value system, and used a sexagesimal numeral system, still in use today for measuring angles and time.[9]
Beginning in the 6th century BC with the Pythagoreans, the Ancient Greeks began a systematic study of mathematics as a subject in its own right with Greek mathematics.[10] Around 300 BC, Euclid introduced the axiomatic method still used in mathematics today, consisting of definition, axiom, theorem, and proof. His textbook Elements is widely considered the most successful and influential textbook of all time.[11] The greatest mathematician of antiquity is often held to be Archimedes (c. 287–212 BC) of Syracuse.[12] He developed formulas for calculating the surface area and volume of solids of revolution and used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, in a manner not too dissimilar from modern calculus.[13] Other notable achievements of Greek mathematics are conic sections (Apollonius of Perga, 3rd century BC),[14] trigonometry (Hipparchus of Nicaea (2nd century BC),[15] and the beginnings of algebra (Diophantus, 3rd century AD).[16]
Chinese mathematics also advanced significantly during this period, primarily motivated by practical problems and less focussed on rigorous proof, in contrast to Greek mathematics. The Nine Chapters on the Mathematical Art, written during the Han dynasty by unknown authors, is often held to be the most significant text of this period. It covers problems such as finding areas of shapes, summing (finite) arithmetic and geometric sums, the solutions of simultaneous linear equations, and contains a version of the Pythagorean theorem. The method described in Chapter 8 for solving systems of linear equations has been compared to Gaussian elimination using matrices,[17] a method which wouldn't be discovered in Europe until well over a millenium later. Liu Hui provided extensive commentaries on the Nine Chapters, extending its methods, as well as developing an algorithm for calculating the value of pi,[18] which would later be used by Zu Chongzhi to calculate pi to seven decimal places,[19] a value significantly more accurate than Western mathematicians of the time.
Post-classical and medieval mathematics[edit]

The Hindu–Arabic numeral system and the rules for the use of its operations, in use throughout the world today, evolved over the course of the first millennium AD in India and were transmitted to the Western world via Islamic mathematics. This period also saw the first use of zero as a number itself, rather than as the absence of a number. Other notable developments of Indian mathematics include the modern definition of sine and cosine, and an early form of infinite series. These developments eventually made their way as far as China and Europe.
During the Golden Age of Islam, especially during the 9th and 10th centuries, mathematics saw many important innovations building on Greek mathematics. The most notable achievement of Islamic mathematics was the development of algebra. Other notable achievements of the Islamic period are advances in spherical trigonometry and the addition of the decimal point to the Arabic numeral system. Many notable mathematicians from this period were Persian, such as Al-Khwarismi, Omar Khayyam and Sharaf al-Dīn al-Ṭūsī.
Arabic and Indian mathematics were introduced to Europe during the high middle ages, with Fibonacci being the most prominent European mathematician of the period. In his book Liber Abaci, Fibonacci popularised the use of the Arabic numeral system,[20] as well as performing perhaps the earliest example of mathematical biology, introducing the Fibonacci sequence to model the population growth of rabbits. Although the Fibonacci sequence had been studied by Indian mathematicians hundreds of years ago,[21] this was the first time it was introduced to Europe, and the first time it was used to solve this problem.
Chinese mathematics at this time also developed rapidly. Following the Indian mathematicians, whose works had by then been translated into Chinese, Chinese mathematicians applied trigonometry to solving problems of chords and arcs in circles,[22] as well as developing spherical trigonometry in the thirteenth century. Chinese algebra also reached a sophisticated level, with Zhu Shijie developing methods to systems of nonlinear polynomials in his text Jade Mirror of the Four Unknowns,[23] using a method now known as Horner's method, which wouldn't be discovered in Europe until the eighteenth century. In order to do this, Zhu also used a version of Pascal's triangle, anticipating another European discovery by centuries.
Renaissance and early modern mathematics[edit]
The European renaissance saw the discovery of general solutions to cubic and quartic equations by Italian mathematicians such as Gerolamo Cardano, Scipio del Ferro and Lodovico Ferrari, achievements which were first published by Cardano in his Ars Magna (in English, "Great Art"), though many of the results were already known. Implicit in these methods is the existence of imaginary numbers, which are necessary for solving general cubic equations, though mathematicians were reluctant to accept their validity outside of this narrow context. Cardano also began the study of probability theory in his work Liber de Ludo Aleae.
This period also saw the invention of two vital tools by René Descartes: Cartesian coordinates, the concept of describing points in space as lists of numbers, and modern algebraic notation, describing equations using symbols rather than words. These two concepts allowed mathematics to develop very rapidly in the seventeenth century, and they were quickly adopted by other mathematicians. Other French mathematicians such as Pierre de Fermat and Marin Mersenne made developments in number theory, studying properties of prime numbers, as well as modular arithmetic and Diophantine equations, which are equations with whole number solutions. The most famous problem involving Diophantine equations from this period is Fermat's last theorem, which remained unsolved for almost 350 years.
The discovery of calculus is considered by many to be the most significant event in seventeenth century mathematics. Although it had its roots as far back as Archimedes, and mathematicians such as Pierre de Fermat and John Wallis had come up with ideas similar to both derivatives and integrals a few decades prior to Newton and Leibniz,[24][25] Newton and Leibniz extended these constructions greatly, demonstrated the link between them (through the fundamental theorem of calculus), and introduced the modern notation for calculus.[a] As well as having tremendous importance in pure mathematics, this also spurred the development of mathematical physics, as now the motion of objects could be described using calculus. Calculus (chiefly in the form developed by Leibniz) was soon developed further by many other mathematicians, most notably Jakob Bernoulli and Johann Bernoulli. The latter tutored Guillaume de l'Hôpital, who published the first calculus textbook, Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes.[26]
Japanese mathematics, known as wasan (written as 和算 using kanji), also began to flourish towards the end of the seventeenth century, largely due to the influence of Seki Takakazu. This development happened almost entirely independently of Western mathematics of the time, though many advances mirrored developments in Europe. Building on the achievements of Chinese mathematics, Seki invented a system of algebraic notation, using kanji to represent unknown quantities. In his Hatsubi Sanpou, published in 1674, he used this to solve systems of equations of arbitrary degree, one even being of degree 1458. He also calculated pi to ten decimal places.[27]
18th century mathematics[edit]

Motivated by problems in physics, the eighteenth century saw many important developments in the study of partial differential equations, equations which describe the rate of change of one variable with respect to many others. Notable mathematicians in this area were Jean le Rond d'Alembert, who discovered the one-dimensional wave equation, Joseph Fourier who worked on the heat equation and developed the notion of Fourier series in the process, Pierre-Simon Laplace, who discovered Laplace's equation, and Leonhard Euler, who discovered the three-dimensional wave equation. The calculus of variations and Lagrangian mechanics, both important tools in applied mathematics, were developed in this time period by Joseph-Louis Lagrange.
The study of statistics grew into its modern form in the eighteenth century.[b] After the introduction of the term statistics to describe studies of the demographics of various states for the Treaty of Westphalia in 1749, many of the core concepts of the modern discipline solidified. John Arbuthnot is credited with the first use of significance tests in 1710, while studying the ratio of male to female births in London over the previous 81 years.[28] In 1761, the reverend Thomas Bayes published Bayes' theorem, which is foundational to the study of conditional probability. The study of probability distributions also came to prominence in this period, most notably due to the work of Laplace. Laplace studied several distributions, most notable among them the Laplace distribution in 1774 and the normal distribution in 1778. The latter of these was independently rediscovered by Gauss in 1795, and is sometimes named the Gaussian distribution in his honor.
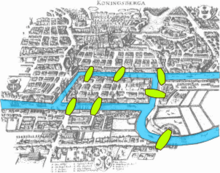
Pure mathematics also developed in Europe, with many advances being the work of Leonhard Euler. His prolific publishing and remarkable breadth of achievement meant that Euler was responsible for many uses of notation that are now standard, among them the use of the Greek letter π for the ratio of a circle's circumference to its diameter, and the use of i for the square root of minus one. Euler invented the subject of graph theory, by setting and then solving the Seven Bridges of Königsberg problem, and also began the study of what is now called topology, by introducing Euler's formula for polyhedra, defining the genus of a surface. Euler was also key to the theory of power series (providing an expression of the zeta function as a product of primes, and solving the Basel problem), number theory (for Euler's theorem, the Euclid–Euler theorem about even perfect numbers, and his conjecture of quadratic reciprocity) and the field that would become complex analysis (through Euler's formula).
In eighteenth century Europe, a culture of awarding mathematical prizes developed. A committee of mathematicians would set an open research problem, and other mathematicians would compete to solve the problem to the committee's satisfaction, with the winner being awarded a monetary prize or a medal. This is somewhat different from the way most mathematics prizes are awarded in the modern day: the subject for which the prize is being awarded is generally no longer specified before the award is given.
19th century mathematics[edit]

The mathematics of the nineteenth century can be characterised by a return to the rigor typified by the ancient Greeks, as compared to early modern or enlightenment mathematics. Its other notable feature is that of increasing abstraction: many features of earlier mathematics (in particular geometry and calculus) pertained to phenomena that could be visualised reasonably well. The greater emphasis on formalism and rigorous proof in the nineteenth century allowed mathematicians to make progress without requiring visual intuition of the objects they studied, allowing for greater abstraction (though intuition would remain a useful tool).
Geometry was one such area in which this increasing abstraction was most apparent. Non-Euclidean geometry, the study of spaces where Euclid's fifth postulate does not hold,[c] was developed by Nikolai Lobachevsky, János Bolyai and Gauss, among others. Gauss created the field of differential geometry, the study of calculus on shapes, and in particular developed intrinsic geometry, studying properties of shapes such as curvature without needing to reference the space they lived in. These developments were expanded upon by Bernhard Riemann, who introduced the notion of a Riemann surface, as well as other objects of vital importance in differential geometry. Other areas of geometry also flourished, notably projective geometry, revived by Jean-Victor Poncelet, which studies shapes in spaces which allow "points at infinity". This spurred the development of algebraic geometry, the geometric study of polynomial functions. Riemann also built on this, eventually culminating in the Riemann-Roch theorem, alongside his student Gustav Roch.
The nineteenth century saw the birth of modern abstract algebra, the study of structure. It grew from the study of roots of polynomial equations; a key problem of European mathematics ever since Cardano's day had been the search for a quintic formula, a formula which would output the solutions of a quintic equation when given the coefficients. The Abel-Ruffini theorem showed that this was impossible, and the short-lived Évariste Galois later proved the stronger result that there exist polynomials of every degree five or greater which cannot be solved by radicals. In order to do this, he introduced the idea of a permutation group, the set of ways of rearranging a set of objects. The more general definition of an abstract group followed later, which allowed for a more rigorous and coherent way for mathematicians to describe symmetries of objects, through group actions. The Irish mathematician William Rowan Hamilton invented quarternions, inscribing the defining statement of them on Broom Bridge in Dublin. These would later become a key example of a division algebra, and would be important to the study of abstract algebra, analysis and physics.[29] Towards the end of the century, Sophus Lie would combine differential geometry with group theory by defining Lie groups, which he did in order to create a form of Galois theory for differential equations. The continuity expressed by the geometric structure combined with the symmetry-encoding properties of the group structure made Lie groups very useful for continuous symmetries, such as those arising in mathematical physics.
Number theory advanced in several different ways during this century. Gauss developed his theorem of quadratic reciprocity, and proved Fermat's last theorem in the n=3 case, both achievements in algebraic number theory. His student Riemann would go on to revolutionise the subject of analytic number theory in his 1859 paper On the Number of Primes Less Than a Given Magnitude, despite this being his only paper on the subject. In this paper, Riemann showed that an "error-correcting term" for an estimate of π(n), the function which counts the number of primes less than n, was linked to the zeroes of the Riemann zeta function. He further conjectured that all of the zeroes of the zeta function would have real part 1/2, his famous Riemann hypothesis, one of the most famous unsolved problems in all of mathematics. In the same paper, Riemann also pioneered important techniques of complex analysis, such as analytic continuation. In the second half of the nineteenth century, Richard Dedekind would develop ring theory and field theory in order to solve problems in algebraic number theory.
Mathematical analysis also underwent drastic changes over the course of the nineteenth century. French mathematician Augustin-Louis Cauchy almost single-handedly invented modern complex analysis during the first half of the century, with Bernhard Riemann and others building upon his results later. Calculus was finally given a rigorous justification by Karl Weierstrass's ε—δ definition of a limit. This definition came with the side-effect of creating some "pathological examples", examples of objects which obey a definition but do not behave how one would expect. For example, Weierstrass constructed the Weierstrass function, which is continuous everywhere but differentiable nowhere. Dedekind also managed to construct the real numbers in a rigorous way, using Dedekind cuts. The tools of calculus, paricularly multivariable and vector calculus, also became much more sophisticated in this period, with such innovations as Green's theorem, Stokes' theorem and Gauss' divergence theorem. The modern notation for vector calculus was developed in the latter half of the century by Josiah Willard Gibbs, who also introduced the dot product and cross product of two vectors. Oliver Heaviside also made significant contributions to the modern study of vector calculus, most notably putting Maxwell's equations into their modern form.[d]
In the late nineteenth century, mathematicians began to be concerned with the foundations of mathematics, the system of axioms and deduction rules with which theorems are proven. Georg Cantor laid the foundations of set theory in the 1870s, as well as introducing the revolutionary idea of transfinite cardinals. Cantor's ideas were deeply controversial, attracting the ire not only of mathematicians such as Leopold Kronecker,[30] but also from philosophers such as Ludwig Wittgenstein.[31] Nonetheless, other mathematicians such as David HIlbert praised his work, famously saying "No one shall expel us from the paradise that Cantor has created."[32] Other mathematicians would eventually come around to Cantor's point of view, and set theory is now the most common way to express many ideas in pure mathematics.
Towards the end of the nineteenth century, the University of Göttingen emerged as the center of the mathematical world, so much so that German had become the de facto international language of mathematics, and native English speakers were publishing their theses in German. This was thanks to the presence there of mathematicians such as Riemann, Dirichlet, Richard Dedekind and Hermann Schwarz.
20th and 21st century mathematics[edit]
Like nineteenth century mathematics, twentieth century mathematics can also be characterised by rapidly increasing abstraction. One notable difference between the two eras is the divergence of different fields. It is sometimes claimed the Henri Poincaré, who was most active in mathematics at the end of the nineteenth century, was the "last universalist",[33] the last mathematician who was able to contribute to all areas of mathematics that existed during his lifetime. After this, the mathematical community was too large, and developments were happening too quicklly, for a single person to keep up with the state of the art in all fields simultaneously.

David Hilbert was the pre-eminent mathematician at the dawn of the twentieth century, contributing to many areas, including algebraic geometry, functional analysis, and mathematical physics. In a speech at the 1900 International Congress of Mathematicians, Hilbert laid out a list of twenty three problems which he viewed as being the most significant at the time. One of Hilbert's chief concerns was on the foundations of mathematics. Hilbert sought to find a system of axioms with which every true statement could be proven, but Kurt Gödel eventually showed that this would be impossible by publishing his incompleteness theorems, which show that any axiomatic system that is consistent will contain unprovable propositions. Alan Turing and Alonzo Church answered Hilbert's halting problem in the negative: there is no algorithm that can determine in finite time whether or not it halts. Turing's idea of a universal computing machine was the theoretical groundwork upon which the discipline of computer science would later be built.
Twentieth century algebraic geometry is marked by its strong trend towards abstraction. The late nineteenth and early twentieth century Italian school of algebraic geometry was relatively grounded in it mathematics, and was typified by an "intuitive" style of proof, which some criticised for its perceived lack of rigor. However, in the postwar period, category theory was invented, which unified many different algebraic and analytic ideas by generalizing to a high level of abstraction. French mathematicians, led by Alexander Grothendieck and the Bourbaki group, utilised and built upon this theory, losing the direct geometric intuition of previous algebraic geometry, but gaining powerful tools in the process. The wide applicability of their ideas, despite their abstraction, stands testament to their success: modern algebraic geometry has applications ranging from string theory to cryptography.
In the early twentieth century, Emmy Noether made wide-reaching changes in abstract algebra. Her early work concerned the theory of invariants, which lead to her proof of Noether's theorem, a conservation law that is one of the most important theorems in mathematical physics. She also did important work on both commutative and noncommutative algebra. The former of these formed the foundations of twentieth century algebraic geometry. Contemporaries such as Albert Einstein described her as "the greatest woman in mathematics".[34] As well as commutative algebra, group theory also continued to develop, in particular the theory of finite groups, culminating in the 1980s with completion of the classification of finite simple groups. This was a colossal task, involving the work of dozens of mathematicians over the course of several decades. The final proof of the classification is estimated to be over 12,000 pages long, though many parts of the proof overlap, as the proof consists of several hundred books, articles and conference proceedings, many of which were not deliberately published as part of an overarching proof. The research of many modern-day group theorists is directed towards simplifying and rewriting the proof of the classification, though the rewrite is still predicted to be thousands of pages long once finished.

Topology also grew more abstract, expanding its scope from the study of manifolds to more general topological spaces. Modern topology is generally held to have started with Poincaré's influential 1895 paper Analysis situs, which he published five supplements to between 1899 and 1904. This generalization made topology an incredibly useful tool in almost all areas of pure mathematics, from geometry to combinatorics. The first half of the twentieth century saw the application of algebraic and differential methods to topology, giving birth to the fields of algebraic and differential topology respectively. These, in turn, then became vital tools for the study of other areas of pure mathematics; algebraic topology was the initial motive behind category theory, and tools such as homotopy and cohomology which were applied in geometry and algebra. Arising from differential topology, the notion of a fibre bundle later became indispensable to the area of physics called gauge theory. Topology was not only studied for its applications to other areas, but was also a highly active area of research in its own right throughout the twentieth century. Major developments in the area are the development of knot theory, the Poincaré conjecture and Thurston's geometrization conjecture (despite still being called conjectures, the last two have both now been proven).
Number theory, like most other areas of mathematics, continued to grow substantially throughout the twentieth century. Key developments were made in the early twentieth century by G. H. Hardy and John Edensor Littlewood, publishing jointly under their idiosyncratic "Hardy–Littlewood rules", which dictated, among other things, that any papers either of them published were to be published jointly, even if one of them had "not contributed the least bit".[35] Hardy is also known for "discovering" Srinivasa Ramanujan, who sent letters to Hardy at Cambridge. The two collaborated on many topics in number theory, before Ramanujan's untimely death in 1920. Another key development is "monstrous moonshine", an eventually-proven conjecture about connections between number-theoretic objects called j-functions and a group called the monster group, the largest sporadic simple group. An important, but less complete area of research is the Langlands program, named after Robert Langlands, a broad set of conjectures which aims to prove deep connections between number theory, group theory and algebraic geometry. Possibly the most significant development in number theory in the twentieth century came right towards the end: in 1995, Andrew Wiles was finally able to prove Fermat's last theorem, building on the work of Yutaka Taniyama, Goro Shimura, and Ken Ribet, among many others. Wiles' proof is considered one of the high points of twentieth century mathematics.
The invention of computers had a profound impact on both pure and applied mathematics. Initially used to break codes during the second world war, the ability to perform computations far faster than any human saw the rapid development of numerical methods for solving problems which were previously intractable. The mathematical modelling of complex phenomena such as weather patterns was now possible. The area of discrete mathematics both benefitted from and contributed to various areas of computer science. This even led in 1976 to the first proof performed by a computer, of the four color theorem. The proof had been divided by human mathematicians into 1,936 separate cases that needed to be checked, which were then checked by computer using code written by Kenneth Appel and Wolfgang Haken. In the modern day, both pure and applied mathematicians frequently use computers for solving numerical problems, as well as checking proofs using automated proof-checking software such as Coq. A very large area of research mathematics is focussed on developing better algorithms for use by computers.
The twentieth century also saw the dispersion of modern mathematics research outside of Western Europe. In the East, Japanese mathematicians such as geometer Kunihiko Kodaira and group theorist Michio Suzuki made fundamental contributions to geometry and algebra, and the Chinese mathematician Shiing-Shen Chern is often considered one of the greatest mathematicians of the twentieth century. Likewise, Srinivasa Ramanujan was a mostly autodidactic Indian mathematician who had a remarkable ability to come up with formulae, and had a very fruitful collaboration with British mathematician G. H. Hardy. Mathematics also shifted Westwards from Europe during and after the second world war. After the Nazi party came to power in Germany in 1933, they sought to purge German universities of what they called "Jewish mathematics", by expelling Jewish academics.[36] The effect was pronounced, particularly at Göttingen (which by this point had become the symbol of German mathematics), and as a result many academics (including Emmy Noether, Emil Artin, Albert Einstein and Richard Courant) fled to the United States. Even after the war was over, many chose to remain in the US, and Göttingen never recovered its former glory. The Soviet Union was also very strong in mathematics, though travel prohibitions on Soviet academics meant that communication between the Soviet bloc and the West was slow.

The Fields medal was established in 1936 by John Charles Fields, and is now often considered to be the highest prize in mathematics.[37] It is often described as "the Nobel prize in mathematics",[38] but in fact even fewer Fields medals are awarded than Nobel prizes in physics: there are up to three Nobel prizes awarded in physics each year, but only up to four Fields medals once every four years. Furthermore, Fields medals are restricted to those who are under the age of forty, while Nobel prizes have no age restriction. The Fields medal was first awarded in 1936 to Lars Ahlfors and Jesse Douglas. The outbreak of the second world war caused great disruption in the mathematics community, and the next medals were not awarded until 1950, though they have been presented once every four years since then.
In 2000, the Clay Mathematics Institute offered a prize of $1,000,000 USD for solving one of a set of seven problems.[39] These problems, called the Millennium prize problems, were chosen by a board of directors as being the most significant problems facing mathematicians at the dawn of the twenty-first century. The problems were: the Poincaré conjecture, the Hodge conjecture, the Birch and Swinnerton-Dyer conjecture, Yang–Mills existence and mass gap, Navier–Stokes existence and smoothness, P vs. NP, and the Riemann hypothesis. As of 2019, only one of the problems has been solved: Grigori Perelman solved the Poincaré conjecture in 2006. However, he turned down the prize money, on the basis that Richard S. Hamilton had done (in Perelman's view) more work towards solving the problem, even if Perelman had been the one to actually prove the conjecture.[40]
Mathematical discoveries continue to be made to this day. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviews database since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs."[41]
Notes[edit]
- ^ See also: History of calculus.
- ^ See also: History of Statistics.
- ^ Euclid's fifth postulate states that for any straight line, and any point not on that line, there is precisely one line through the point which does not intersect the first line. In spherical geometry, there are no lines which do not intersect the first line, and in hyperbolic geometry, there is more than one line which does not intersect the first.
- ^ Previously, they had been a set of twenty equations in twelve unknowns described using quarternions. Heaviside expressed them in modern vector calculus notation, and in doing so reduced them to four equations.
References[edit]
- ^ Dehaene, Stanislas; Dehaene-Lambertz, Ghislaine; Cohen, Laurent (Aug 1998). "Abstract representations of numbers in the animal and human brain". Trends in Neurosciences. 21 (8): 355–61. doi:10.1016/S0166-2236(98)01263-6. PMID 9720604.
- ^ "mathematic". Online Etymology Dictionary. Archived from the original on March 7, 2013.
- ^ Both meanings can be found in Plato, the narrower in Republic 510c, but Plato did not use a math- word; Aristotle did, commenting on it. μαθηματική. Liddell, Henry George; Scott, Robert; A Greek–English Lexicon at the Perseus Project. OED Online, "Mathematics".
- ^ Boas, Ralph (1995) [1991]. "What Augustine Didn't Say About Mathematicians". Lion Hunting and Other Mathematical Pursuits: A Collection of Mathematics, Verse, and Stories by the Late Ralph P. Boas, Jr. Cambridge University Press. p. 257. ISBN 9780883853238.
- ^ The Oxford Dictionary of English Etymology, Oxford English Dictionary, sub "mathematics", "mathematic", "mathematics"
- ^ "maths, n." and "math, n.3". Oxford English Dictionary, on-line version (2012).
- ^ See, for example, Raymond L. Wilder, Evolution of Mathematical Concepts; an Elementary Study, passim
- ^ Kline 1990, Chapter 1.
- ^ Boyer 1991, "Mesopotamia" p. 24–27.
- ^ Heath, Thomas Little (1981) [originally published 1921]. A History of Greek Mathematics: From Thales to Euclid. New York: Dover Publications. ISBN 978-0-486-24073-2.
- ^ Boyer 1991, "Euclid of Alexandria" p. 119.
- ^ Boyer 1991, "Archimedes of Syracuse" p. 120.
- ^ Boyer 1991, "Archimedes of Syracuse" p. 130.
- ^ Boyer 1991, "Apollonius of Perga" p. 145.
- ^ Boyer 1991, "Greek Trigonometry and Mensuration" p. 162.
- ^ Boyer 1991, "Revival and Decline of Greek Mathematics" p. 180.
- ^ Hart, Roger (2011). The Chinese Roots of Linear Alegbra. Johns Hopkins University. pp. 11–85. ISBN 978-0801897559.
- ^ Shuchun, Guo, The Nine Chapters on Mathematical Procedures and Liu Hui's Mathematical Theory, (Seki 2013, pp. 63–89).
- ^ Bailey et al. (1997)
- ^ Sigler, Laurence E. (trans.) (2002), Fibonacci's Liber Abaci, Springer-Verlag, ISBN 0-387-95419-8
- ^ Singh 1985.
- ^ Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.
- ^ Shirong, Guo, "The Axes of Mathematical Methodology in the Song and Yuan Dynasties: The Construction of Mathematical Models", Seki (2013, pp. 105–118).
- ^ Pellegrino, Dana. "Pierre de Fermat". Retrieved 2008-02-24.
- ^ Joseph Frederick Scott, The mathematical work of John Wallis (1616–1703), Taylor and Francis, 1938.
- ^ Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes at the Internet archive.
- ^ Takenouchi, Osamu, "Résumé of Works on Mathematics of Seki Takakazu", Seki (2013, pp. 187–192).
- ^ John Arbuthnot (1710). "An argument for Divine Providence, taken from the constant regularity observed in the births of both sexes" (PDF). Philosophical Transactions of the Royal Society of London. 27 (325–336): 186–190. doi:10.1098/rstl.1710.0011.
- ^ Girard, P. R. (1984). "The quaternion group and modern physics". European Journal of Physics. 5 (1): 25–32. Bibcode:1984EJPh....5...25G. doi:10.1088/0143-0807/5/1/007.
- ^ Dauben, Joseph Warren (1979). Georg Cantor His Mathematics and Philosophy of the Infinite. princeton university press. pp. introduction. ISBN 9780691024479.
- ^ Dauben 1979, pp. 120, 143
- ^ Reid, Constance (1996), Hilbert, New York: Springer-Verlag, p. 177, ISBN 978-0-387-04999-1
- ^ Ginoux, J. M.; Gerini, C. (2013). Henri Poincaré: A Biography Through the Daily Papers. World Scientific. doi:10.1142/8956. ISBN 978-981-4556-61-3.
- ^ Einstein, Albert (1 May 1935), "Professor Einstein Writes in Appreciation of a Fellow-Mathematician", The New York Times (published 5 May 1935), retrieved 13 April 2008
- ^ Teixeira da Silva, Jaime; Dobránszki, Judit (2013). "Should the Hardy–-Littlewood Axioms of Collaboration be Used for Collaborative Authorship?". The Asian and Australasian Journal of Plant Science and Biotechnology. 7: 72–75.
- ^ Böhme, Ernst. "History of the University - an overview". University of Göttingen. Retrieved 29 July 2019..
- ^ "Top Award, ShanghaiRanking Academic Excellence Survey 2017 | Shanghai Ranking - 2017". Shanghairanking.com. Retrieved 2018-03-29.
- ^ Ball, Philip (2014). "Iranian is first woman to nab highest prize in maths". Nature. doi:10.1038/nature.2014.15686.
- ^ "The Millennium Prize Problems". Clay Mathematics Institute. Retrieved 10 July 2019.
- ^ Malcolm Ritter (July 1, 2010). "Russian mathematician rejects $1 million prize". AP on PhysOrg. Archived from the original on January 17, 2012. Retrieved May 15, 2011.
- ^ Sevryuk 2006, pp. 101–09.
Bibliography[edit]
- Bailey, David H.; Borwein, Jonathan M.; Borwein, Peter B.; Plouffe, Simon (1997). "The quest for pi" (PDF). Mathematical Intelligencer. 19 (1): 50–57. doi:10.1007/BF03024340.
- Knobloch, Eberhard; Komatsu, Hikosaburo; Liu, Dun, eds. (2013). "Seki, Founder of Modern Mathematics in Japan: A Commemoration on His Tercentenary". Seki, Founder of Modern Mathematics in Japan. Springer. ISBN 978-4-431-54273-5.
- Singh, Pamanand (1985). "The so-called fibonacci numbers in ancient and medieval India". Historia Mathematica. 12 (3): 229–244. doi:10.1016/0315-0860(85)90021-7.
