User:Physicsyang25/sandbox

Quantum mechanics

Possible eigenvalues

Two dimensional representations of parity are given by a pair of quantum states which go into each other under parity. However, this representation can always be reduced to linear combinations of states, each of which is either even or odd under parity. One says that all irreducible representations of parity are one-dimensional.

In quantum mechanics, spacetime transformations act on quantum states. The parity transformation, ${\hat {\mathcal {P}}}$, is a unitary operator, in general acting on a state $\psi$ as follows: ${\hat {\mathcal {P}}}\,\psi _{\left(r\right)}=e^{\frac {i\phi }{2}}\psi _{\left(-r\right)}$.

One must then have ${\hat {\mathcal {P}}}^{2}\,\psi _{\left(r\right)}=e^{i\phi }\psi _{\left(r\right)}$, since an overall phase is unobservable. The operator ${\hat {\mathcal {P}}}^{2}$, which reverses the parity of a state twice, leaves the spacetime invariant, and so is an internal symmetry which rotates its eigenstates by phases $e^{i\phi }$. If ${\hat {\mathcal {P}}}^{2}$ is an element $e^{iQ}$ of a continuous U(1) symmetry group of phase rotations, then $e^{-iQ}$is part of this U(1) and so is also a symmetry. In particular, we can define ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{\frac {iQ}{2}}}$, which is also a symmetry, and so we can choose to call ${\hat {\mathcal {P}}}'$ our parity operator, instead of ${\hat {\mathcal {P}}}^{2}$. Note that ${{\hat {\mathcal {P}}}'}^{2}=1$ and so ${\hat {\mathcal {P}}}'$ has eigenvalues $\pm 1$. Wave functions with eigenvalue +1 under a parity transformation are even functions, while eigenvalue -1 corresponds to odd functions. However, when no such symmetry group exists, it may be that all parity transformations have some eigenvalues which are phases other than $\pm 1$.

For electronic wavefunctions, even states are usually indicated by a subscript g for gerade (German: even) and odd states by a subscript u for ungerade (German: odd). For example, the lowest energy level of the hydrogen molecule ion (H₂⁺) is labelled $1\sigma _{g}$ and the next-closest (higher) energy level is labelled $1\sigma _{u}$.

The wave functions of a particle moving into an external potential, which is centrosymmetric (potential energy invariant with respect to a space inversion, symmetric to the origin), either remain invariable or change signs: these two possible states are called the even state or odd state of the wave functions.

The law of conservation of parity of particle (not true for the beta decay of nuclei) states that, if an isolated ensemble of particles has a definite parity, then the parity remains invariable in the process of ensemble evolution.

The parity of the states of a particle moving in a spherically symmetric external field is determined by the angular momentum, and the particle state is defined by three quantum numbers: total energy, angular momentum and the projection of angular momentum.

Consequences of parity symmetry

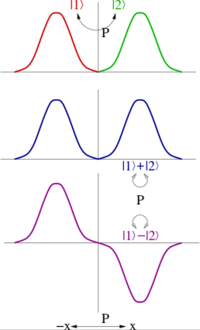
When parity generates the Abelian group ℤ₂, one can always take linear combinations of quantum states such that they are either even or odd under parity (see the figure). Thus the parity of such states is ±1. The parity of a multiparticle state is the product of the parities of each state; in other words parity is a multiplicative quantum number.

In quantum mechanics, Hamiltonians are invariant (symmetric) under a parity transformation if ${\hat {\mathcal {P}}}$ commutes with the Hamiltonian. In non-relativistic quantum mechanics, this happens for any potential which is scalar, i.e., $V=V{\left(r\right)}$, hence the potential is spherically symmetric. The following facts can be easily proven:

• If $\left|\varphi \right\rangle$ and $\left|\psi \right\rangle$ have the same parity, then $\left\langle \varphi \right|{\hat {X}}\left|\psi \right\rangle =0$ where ${\hat {X}}$ is the position operator.
• For a state $\left|{\vec {L}},L_{z}\right\rangle$ of orbital angular momentum ${\vec {L}}$ with z-axis projection $L_{z}$, then ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$.
• If $\left[{\hat {H}},{\hat {P}}\right]=0$, then atomic dipole transitions only occur between states of opposite parity.
• If $\left[{\hat {H}},{\hat {P}}\right]=0$, then a non-degenerate eigenstate of ${\hat {H}}$ is also an eigenstate of the parity operator; i.e., a non-degenerate eigenfunction of ${\hat {H}}$ is either invariant to ${\hat {\mathcal {P}}}$ or is changed in sign by ${\hat {\mathcal {P}}}$.

Some of the non-degenerate eigenfunctions of ${\hat {H}}$ are unaffected (invariant) by parity ${\hat {\mathcal {P}}}$ and the others will be merely reversed in sign when the Hamiltonian operator and the parity operator commute:

${\hat {\mathcal {P}}}\left|\psi \right\rangle =c\left|\psi \right\rangle$,

where $c$ is a constant, the eigenvalue of ${\hat {\mathcal {P}}}$,

${\hat {\mathcal {P}}}^{2}\left|\psi \right\rangle =c\,{\hat {\mathcal {P}}}\left|\psi \right\rangle$.

量子力學

特徵值

在量子力學中時空變換是作用在量子態上的。宇稱變換 ${\hat {\mathcal {P}}}$ 是一種么正算符，其對量子態的作用如下所示： ${\hat {\mathcal {P}}}\,\psi _{\left(r\right)}=e^{\frac {i\phi }{2}}\psi _{\left(-r\right)}$.