User:Jim.belk/Draft of Hyperbolic Geometry

hello

A perspective projection of a dodecahedral tessellation, {5,3,4}, in H³.
Four dodecahedra meet at each edge, and eight meet at each vertex, just like a cubic tessellation in E³

A Poincaré disc model of {5,4} tiling in H². Four pentagons meet at each vertex, just like a square tiling in E²

In mathematics, hyperbolic geometry is the geometry of the hyperbolic plane and hyperbolic n-space. Historically, hyperbolic geometry arose as a non-Euclidean geometry for which the parallel postulate fails. It has since become a become a basic tool in the study of manifolds, infinite discrete groups, automorphic forms, and conformal structures.

History

See also: Non-Euclidean Geometry

Hyperbolic geometry first arose out of attempts to prove the parallel postulate from the other four postulates of Euclidean geometry. In the 11th century, Omar Khayyám[1] attempted to prove the parallel postulate by contradiction, but was unable to find an inconsistency with the other four axioms. Italian mathematician Giovanni Girolamo Saccheri also struggled in vain to derive a contradiction from the negation of the parallel postulate. By the early 19th century, Karl Friedrich Gauss, János Bolyai, and Nikolai Ivanovich Lobachevsky each came to the conclusion that the negation of the parallel postulate was consistent with the other axioms of geometry. Gauss neglected to publish his work, but Lobachevski and Bolyai managed to popularize the new system as a non-Euclidean version of geometry. (There continues to be some dispute over the priority of this discovery.)

In 1868, Eugenio Beltrami constructed several models of hyperbolic geometry in the Euclidean plane. This proved the consistency of hyperbolic geometry, assuming that Euclidean geometry is itself consistent (see [models of the hyperbolic plane] below). In 1871, Felix Klein showed that Euclidean and non-Euclidean geometries could be considered special cases of a projective surface with a specific conic section adjoined, thus putting the two geometries on the same logical footing.

Near the turn of the century, Henri Poincaré used hyperbolic geometry extensively in his work on automorphic forms (which he referred to as Fuchsian functions). He developed the theory of Fuchsian and Kleinian groups, thereby establishing the connection betweeen hyperbolic geometry, conformal structures, and Riemann surfaces.

In 1968, G.D. Mostow proved his famous rigidity theorem, which states that the geometry of a finite-volume hyperbolic manifold is determined by its fundamental group. At the time, however, few hyperbolic manifolds were known in dimensions greater than two. In the mid 1970s, Robert Riley and Troels Jørgensen independently proved that the complement of the figure-eight knot was a hyperbolic manifold. This result was soon generalized by William Thurston, who produced a large number of hyperbolic 3-manifolds, and argued successfully that a "typical" 3-manifold is hyperbolic. This work injected hyperbolic geometry into the center of low-dimensional topology.

In 1987, Mikhail Gromov revolutionized group theory with his notion of a hyperbolic group. Roughly speaking, a hyperbolic group is a finitely-generated discrete group whose Cayley graph behaves like a lattice in hyperbolic space. Gromov went on to show that "typical" finitely-presented infinite group is hyperbolic, making the study of hyperbolic groups a fundamental part of geometric group theory.

Models

Main article: hyperbolic space

There are four models commonly used for hyperbolic geometry: the Klein model, the Poincaré disc model, the Poincaré half-plane model, and the Lorentz model, or hyperboloid model. These models define a real hyperbolic space which satisfies the axioms of a hyperbolic geometry.

Poincaré disc model of great rhombitruncated {3,7} tiling

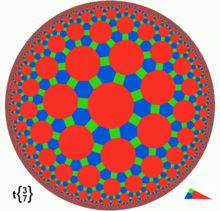
1. The Klein model, also known as the projective disc model and Beltrami-Klein model, uses the interior of a circle for the hyperbolic plane, and chords of the circle as lines.
   • This model has the advantage of simplicity, but the disadvantage that angles in the hyperbolic plane are distorted.
2. The Poincaré disc model, also known as the conformal disc model, also employs the interior of a circle, but lines are represented by arcs of circles that are orthogonal to the boundary circle, plus diameters of the boundary circle.
3. The Poincaré half-plane model takes one-half of the Euclidean plane, as determined by a Euclidean line B, to be the hyperbolic plane (B itself is not included).
   • Hyperbolic lines are then either half-circles orthogonal to B or rays perpendicular to B.
   • Both Poincaré models preserve hyperbolic angles, and are thereby conformal. All isometries within these models are therefore Möbius transformations.
4. A fourth model is the Lorentz model or hyperboloid model, which employs a 2-dimensional hyperboloid of revolution (of two sheets, but using one) embedded in 3-dimensional Minkowski space. This model is generally credited to Poincaré, but Reynolds (see below) says that Wilhelm Killing and Karl Weierstrass used this model from 1872.
   • This model has direct application to special relativity, as Minkowski 3-space is a model for spacetime, suppressing one spatial dimension. One can take the hyperboloid to represent the events that various moving observers, radiating outward in a spatial plane from a single point, will reach in a fixed proper time. The hyperbolic distance between two points on the hyperboloid can then be identified with the relative rapidity between the two corresponding observers.

Hyperparallel lines

An interesting property of hyperbolic geometry follows from allowing more than one parallel line through a point: there are two classes of non-intersecting lines. Let B be the point on l such that the line PB is perpendicular to l. Consider the line x through P such that x does not intersect l, and the angle theta between PB and x (counterclockwise from PB) is as small as possible (i.e., any smaller an angle will force the line to intersect l). This is called a hyperparallel line (or simply parallel line) in hyperbolic geometry. Similarly, the line y that forms the same angle theta between PB and itself but clockwise from PB will also be hyper-parallel, but there can be no others. All other lines through P not intersecting l form angles greater than theta with PB, and are called ultraparallel (or disjointly parallel) lines. Notice that since there are an infinite number of possible angles between theta and 90 degrees, and each one will determine two lines through P and disjointly parallel to l, we have an infinite number of ultraparallel lines.

Thus we have this modified form of the parallel postulate: In Hyperbolic Geometry, given any line l, and point P not on l, there are exactly two lines through P which are hyperparallel to l, and infinitely many lines through P ultraparallel to l.

The differences between these types of lines can also be looked at in the following way: the distance between hyperparallel lines goes to 0 as you move on to infinity. However, the distance between ultraparallel lines does not go to 0 as you move to infinity.

The angle of parallelism in Euclidean geometry is a constant, that is, any length BP will yield an angle of parallelism equal to 90°. In hyperbolic geometry, the angle of parallelism varies with what is called the Π(p) function. This function, described by Nikolai Ivanovich Lobachevsky produced a unique angle of parallelism for each given length BP. As the length BP gets shorter, the angle of parallelism will approach 90°. As the length BP increases without bound, the angle of parallelism will approach 0°. Notice that due to this fact, as distances get smaller, the hyperbolic plane behaves more and more like Euclidean geometry. So on the small scale, an observer within the hyperbolic plane would have a hard time determining they are not in a Euclidean plane.

Visualizing hyperbolic geometry

M. C. Escher's famous prints Circle Limit III and Circle Limit IV illustrate the conformal disc model quite well. In both one can see the geodesics (in III the white lines are not geodesics, but hypercycles, which run alongside them). It is also possible to see quite plainly the negative curvature of the hyperbolic plane, through its effect on the sum of angles in triangles and squares.

For example, in Circle Limit III every vertex belongs to three triangles and three squares. In the Euclidean plane, their angles would sum to 450°, i.e. a circle and a quarter. From this we see that the sum of angles of a triangle in the hyperbolic plane must be smaller than 180°. Another visible property is exponential growth. In Circle Limit IV, for example, one can see that the number of angels within a distance of n from the center rises exponentially. The angels have equal hyperbolic area, so the area of a ball of radius n must rise exponentially in n.

There are several ways to physically realize a hyperbolic plane (or approximation thereof). A particularly well-known paper model based on the pseudosphere is due to William Thurston. The art of crochet has been used to demonstrate hyperbolic planes with the first being made by Daina Taimina. In 2000, Keith Henderson demonstrated a quick-to-make paper model dubbed the "Hyperbolic soccerball."

Relationship to Riemann surfaces

Two-dimensional hyperbolic surfaces can also be understood according to the language of Riemann surfaces. According to the uniformization theorem, every Riemann surface is either elliptic, parabolic or hyperbolic. Most hyperbolic surfaces have a non-trivial fundamental group $\pi _{1}=\Gamma ,$ known as the Fuchsian group. The quotient space H/Γ of the upper half-plane modulo the fundamental group is known as the Fuchsian model of the hyperbolic surface. The Poincaré half plane is also hyperbolic, but is simply connected and noncompact. It is the universal cover of the other hyperbolic surfaces.

The analogous construction for three-dimensional hyperbolic surfaces is the Kleinian model.

See also

• Angle of parallelism
• Elliptic geometry
• Hyperbolic space
• Hyperbolic structure
• Hyperboloid model
• Hyperboloid structure
• Fuchsian group
• Fuchsian model
• Hjelmslev transformation
• Hyperbolic 3-manifold
• Klein model
• Kleinian group
• Kleinian model
• Poincaré disk model
• Poincaré half-plane model
• Poincaré metric
• Riemann surface
• Khayyam-Saccheri quadrilateral
• Special relativity
• Systolic geometry
• Ultraparallel theorem

External links

• Visions of Infinity: Tiling a hyperbolic floor inspires both mathematics and art Science News: Dec. 23, 2000; Vol. 158, No. 26/27, p. 408

• Java freeware for creating sketches in both the Poincaré Disk and the Upper Half-Plane Models of Hyperbolic Geometry University of New Mexico

• "The Hyperbolic Geometry Song" A short music video about the basics of Hyperbolic Geometry available at Youtube.

• Book on Hyperbolic Geometry Google books

• Weisstein, Eric W. "Gauss-Bolyai-Lobachevsky Space". MathWorld.

References

• Reynolds, William F. (1993) "Hyperbolic Geometry on a Hyperboloid", American Mathematical Monthly 100:442-455.
• Stillwell, John. (1996) Sources in Hyperbolic Geometry, volume 10 in AMS/LMS series History of Mathematics.
• Samuels, David. (March 2006) "Knit Theory" Discover Magazine, volume 27, Number 3.