User:Double sharp/List of uniform tilings by Schwarz triangle
Yes, I'm fully aware that this is a misnomer: Schwarz triangles are spherical. I should really be referring to Coxeter polytopes (since we're referring to tilings of E2/H2, I could say Coxeter polygons.)
This is the Euclidean and hyperbolic version of List of uniform polyhedra by Schwarz triangle.
What exactly sabotages {5,10/3}, {5/2,10}, {7,14/5}, {7/2,14/3}, {7/3,14} etc. and makes them have infinite density though they'd fit in the plane? – ah, I see, from Regular Polytopes (3rd ed.), p.108: they would have rotational symmetries that are not 2-, 3-, 4-, or 6-fold, which we know to be impossible.
Basically what we need is:
Add and subtract interior angles of {3} (60°), {4} (90°), {6} (120°), {8} (135°), {8/3} (45°), {12} (150°), {12/5} (30°), {∞} (180°) to yield some multiple of 360°. This will determine a candidate vertex figure. We may reject everything containing consecutive positive and negative terms of the same angle as degenerate. Some candidates may also be excluded by symmetric concerns, such as {8/3, 8} above. (Though we need to prove that only the above tiles are possible.) However such a bald listing ends up creating lots of junk as well...
Summary table[edit]

There are seven generator points with each set of p,q,r (and a few special forms):
| General | Right triangle (r=2) | ||||||
|---|---|---|---|---|---|---|---|
| Description | Wythoff symbol |
Vertex configuration |
Coxeter diagram |
Wythoff symbol |
Vertex configuration |
Schläfli symbol |
Coxeter diagram |
| regular and quasiregular |
q | p r | (p.r)q | q | p 2 | pq | {p,q} | ||
| p | q r | (q.r)p | p | q 2 | qp | {q,p} | |||
| r | p q | (q.p)r | 2 | p q | (q.p)² | t1{p,q} | |||
| truncated and expanded |
q r | p | q.2p.r.2p | q 2 | p | q.2p.2p | t0,1{p,q} | ||
| p r | q | p.2q.r.2q | p 2 | q | p. 2q.2q | t0,1{q,p} | |||
| p q | r | 2r.q.2r.p | p q | 2 | 4.q.4.p | t0,2{p,q} | |||
| even-faced | p q r | | 2r.2q.2p | p q 2 | | 4.2q.2p | t0,1,2{p,q} | ||
| p q (r s) | | 2p.2q.-2p.-2q | - | p 2 (r s) | | 2p.4.-2p.4/3 | - | ||
| snub | | p q r | 3.r.3.q.3.p | | p q 2 | 3.3.q.3.p | s{p,q} | ||
| | p q r s | (4.p.4.q.4.r.4.s)/2 | - | - | - | - | ||
There are three special cases:
- p q (r s) | – This is a mixture of p q r | and p q s |.
- | p q r – Snub forms (alternated) are give this otherwise unused symbol.
- | p q r s – A unique snub form for U75 that isn't Wythoff-constructible.
Euclidean tilings[edit]
The only plane triangles that tile the plane once over are (3 3 3), (4 2 4), and (3 2 6): they are respectively the equilateral triangle, the 45-45-90 right isosceles triangle, and the 30-60-90 right triangle. It follows that any plane triangle tiling the plane multiple times must be built up from multiple copies of one of these. The only possibility is the 30-120-120 isosceles triangle (3/2 6 6) = (6 2 3) + (2 6 3) tiling the plane twice over. Each triangle counts twice with opposite orientations, with a branch point at the 120° vertices.[1]
The tiling {∞,2} made from two apeirogons is not accepted, because its faces meet at more than one edge. Here ∞' denotes the retrograde counterpart to ∞.
The degenerate named forms are:
- chatit: compound of 3 hexagonal tilings + triangular tiling
- chata: compound of 3 hexagonal tilings + triangular tiling + double covers of apeirogons along all edge sequences
- cha: compound of 3 hexagonal tilings + double covers of apeirogons along all edge sequences
- cosa: square tiling + double covers of apeirogons along all edge sequences
| (p q r) | q | p r (p.r)q |
p | q r (q.r)p |
r | p q (q.p)r |
q r | p q.2p.r.2p |
p r | q p.2q.r.2q |
p q | r 2r.q.2r.p |
p q r | 2r.2q.2p |
| p q r 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|
| (6 3 2) |  6.6.6 hexat |
 3.3.3.3.3.3 trat |
 3.6.3.6 that |
 3.12.12 toxat |
 6.6.6 hexat |
 4.3.4.6 srothat |
 4.6.12 grothat |
 3.3.3.3.6 snathat |
| (4 4 2) |  4.4.4.4 squat |
 4.4.4.4 squat |
 4.4.4.4 squat |
 4.8.8 tosquat |
 4.8.8 tosquat |
 4.4.4.4 squat |
 4.8.8 tosquat |
 3.3.4.3.4 snasquat |
| (3 3 3) |  3.3.3.3.3.3 trat |
 3.3.3.3.3.3 trat |
 3.3.3.3.3.3 trat |
 3.6.3.6 that |
 3.6.3.6 that |
 3.6.3.6 that |
 6.6.6 hexat |
 3.3.3.3.3.3 trat |
| (∞ 2 2) | — | — | — | — |  4.4.∞ azip |
 4.4.∞ azip |
 4.4.∞ azip |
3.3.3.∞ azap |
| (3/2 3/2 3) |  3.3.3.3.3.3 trat |
 3.3.3.3.3.3 trat |
 3.3.3.3.3.3 trat |
∞-covered {3} | ∞-covered {3} |  3.6.3.6 that |
[degenerate] | |
| (4 4/3 2) |  4.4.4.4 squat |
 4.4.4.4 squat |
 4.4.4.4 squat |
 4.8.8 tosquat |
 4.8/5.8/5 quitsquat |
∞-covered {4} |  4.8/3.8/7 qrasquit |
|
| (4/3 4/3 2) |  4.4.4.4 squat |
 4.4.4.4 squat |
 4.4.4.4 squat |
 4.8/5.8/5 quitsquat |
 4.8/5.8/5 quitsquat |
 4.4.4.4 squat |
 4.8/5.8/5 quitsquat |
 3.3.4/3.3.4/3 rasisquat |
| (3/2 6 2) |  3.3.3.3.3.3 trat |
 6.6.6 hexat |
 3.6.3.6 that |
[degenerate] |  3.12.12 toxat |
 3/2.4.6/5.4 qrothat |
[degenerate] | |
| (3 6/5 2) |  3.3.3.3.3.3 trat |
 6.6.6 hexat |
 3.6.3.6 that |
 6.6.6 hexat |
 3/2.12/5.12/5 quothat |
 3/2.4.6/5.4 qrothat |
 4.6/5.12/5 quitothit |
|
| (3/2 6/5 2) |  3.3.3.3.3.3 trat |
 6.6.6 hexat |
 3.6.3.6 that |
[degenerate] |  3/2.12/5.12/5 quothat |
 3.4.6.4 srothat |
[degenerate] | |
| (3/2 6 6) |  (3/2.6)6 chatit |
 (6.6.6.6.6.6)/2 2hexat |
 (3/2.6)6 chatit |
[degenerate] |  3/2.12.6.12 shothat |
 3/2.12.6.12 shothat |
[degenerate] | |
| (3 6 6/5) |  (3/2.6)6 chatit |
 (6.6.6.6.6.6)/2 2hexat |
 (3/2.6)6 chatit |
∞-covered {6} |  3/2.12.6.12 shothat |
 3.12/5.6/5.12/5 ghothat |
 6.12/5.12/11 thotithit |
|
| (3/2 6/5 6/5) |  (3/2.6)6 chatit |
 (6.6.6.6.6.6)/2 2hexat |
 (3/2.6)6 chatit |
[degenerate] |  3.12/5.6/5.12/5 ghothat |
 3.12/5.6/5.12/5 ghothat |
[degenerate] | |
| (3 3/2 ∞) |  (3.∞)3/2 = (3/2.∞)3 ditatha |
 (3.∞)3/2 = (3/2.∞)3 ditatha |
— |  6.3/2.6.∞ chata |
[degenerate] |  3.∞.3/2.∞ tha |
[degenerate] | |
| (3 3 ∞') |  (3.∞)3/2 = (3/2.∞)3 ditatha |
 (3.∞)3/2 = (3/2.∞)3 ditatha |
— |  6.3/2.6.∞ chata |
 6.3/2.6.∞ chata |
[degenerate] | [degenerate] | |
| (3/2 3/2 ∞') |  (3.∞)3/2 = (3/2.∞)3 ditatha |
 (3.∞)3/2 = (3/2.∞)3 ditatha |
— | [degenerate] | [degenerate] | [degenerate] | [degenerate] | |
| (4 4/3 ∞) |  (4.∞)4/3 cosa |
 (4.∞)4/3 cosa |
— |  8.4/3.8.∞ gossa |
 8/3.4.8/3.∞ sossa |
 4.∞.4/3.∞ sha |
 8.8/3.∞ satsa |
 3.4.3.4/3.3.∞ snassa |
| (4 4 ∞') |  (4.∞)4/3 cosa |
 (4.∞)4/3 cosa |
— |  8.4/3.8.∞ gossa |
 8.4/3.8.∞ gossa |
[degenerate] | [degenerate] | |
| (4/3 4/3 ∞') |  (4.∞)4/3 cosa |
 (4.∞)4/3 cosa |
— |  8/3.4.8/3.∞ sossa |
 8/3.4.8/3.∞ sossa |
[degenerate] | [degenerate] | |
| (6 6/5 ∞) |  (6.∞)6/5 cha |
 (6.∞)6/5 cha |
— |  6/5.12.∞.12 ghaha |
 6.12/5.∞.12/5 shaha |
 6.∞.6/5.∞ 2hoha |
 12.12/5.∞ hatha |
|
| (6 6 ∞') |  (6.∞)6/5 cha |
 (6.∞)6/5 cha |
— |  6/5.12.∞.12 ghaha |
 6/5.12.∞.12 ghaha |
[degenerate] | [degenerate] | |
| (6/5 6/5 ∞') |  (6.∞)6/5 cha |
 (6.∞)6/5 cha |
— |  6.12/5.∞.12/5 shaha |
 6.12/5.∞.12/5 shaha |
[degenerate] | [degenerate] |
The tiling 6 6/5 | ∞ is generated as a double cover by Wythoff's construction:
 6.∞.6/5.∞ hoha hemi(6 6/5 | ∞) |
Also there are a few tilings with the mixed symbol p q r
s |:
 4.12.4/3.12/11 sraht 2 6 3/2 3 | |
 4.12/5.4/3.12/7 graht 2 6/5 3/2 3 | |
 8/3.8.8/5.8/7 sost 4/3 4 2 ∞ | |
 12/5.12.12/7.12/11 huht 6/5 6 3 ∞ | |
There are also some non-Wythoffian tilings:
 3.3.3.4.4 etrat |
3.3.3.4/3.4/3 retrat |
4.8.8/3.4/3.∞ rorisassa |
4.8/3.8.4/3.∞ rosassa |
4.8.4/3.8.4/3.∞ rarsisresa |
4.8/3.4.8/3.4/3.∞ rassersa |
Hyperbolic[edit]
OK, apparently the hyperbolic fundamental domains are called Lannér triangles (compact) per Coxeter–Dynkin diagram#Hyperbolic Coxeter groups, Koszul triangles (paracompact) and Vinberg triangles (noncompact). But these are only right for simplices, no? So in general I'd write "Coxeter polygons" again.
| (p q r) | q | p r (p.r)q |
p | q r (q.r)p |
r | p q (q.p)r |
q r | p q.2p.r.2p |
p r | q p.2q.r.2q |
p q | r 2r.q.2r.p |
p q r | 2r.2q.2p |
| p q r 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|
| (7 3 2) |  7.7.7 heat |
 3.3.3.3.3.3.3 hetrat |
 3.7.3.7 thet |
 3.14.14 theat |
 6.6.7 thetrat |
 4.3.4.7 srothet |
 4.6.14 grothet |
 3.3.3.3.7 snathet |
| (8 3 2) |  8.8.8 ocat |
 3.3.3.3.3.3.3.3 otrat |
 3.8.3.8 toct |
 3.16.16 tocat |
 6.6.8 totrat |
 4.3.4.8 srotoct |
 4.6.16 grotoct |
 3.3.3.3.8 snatoct |
| (5 4 2) |  5.5.5.5 peat |
 4.4.4.4.4 pesquat |
 4.5.4.5 tepet |
 4.10.10 topeat |
 5.8.8 topesquat |
 4.4.4.5 srotepet |
 4.8.10 grotepet |
 3.3.4.3.5 stepet |
| (6 4 2) |  6.6.6.6 shexat |
 4.4.4.4.4.4 hisquat |
 4.6.4.6 tehat |
 4.12.12 toshexat |
 6.8.8 thisquat |
 4.4.4.6 srotehat |
 4.8.12 grotehat |
 3.3.4.3.6 snatehat |
| (5 5 2) |  5.5.5.5.5 pepat |
 5.5.5.5.5 pepat |
 5.5.5.5 peat |
 5.10.10 topepat |
 5.10.10 topepat |
 4.5.4.5 tepet |
 4.10.10 topeat |
 3.3.5.3.5 spepat |
| (6 6 2) |  6.6.6.6.6.6 hihat |
 6.6.6.6.6.6 hihat |
 6.6.6.6 shexat |
 6.12.12 thihat |
 6.12.12 thihat |
 4.6.4.6 tehat |
 4.12.12 toshexat |
 3.3.6.3.6 shihat |
| (4 3 3) |  3.4.3.4.3.4 dittitecat |
 3.3.3.3.3.3.3.3 otrat |
 3.4.3.4.3.4 dittitecat |
 3.8.3.8 toct |
 6.3.6.4 sittitetrat |
 6.3.6.4 sittitetrat |
 6.6.8 totrat |
 3.3.3.3.3.4 stititet |
| (4 4 3) |  3.4.3.4.3.4.3.4 ditetetrat |
 3.4.3.4.3.4.3.4 ditetetrat |
 4.4.4.4.4.4 hisquat |
 4.8.3.8 sittiteteat |
 4.8.3.8 sittiteteat |
 6.4.6.4 tehat |
 6.8.8 thisquat |
 3.3.3.4.3.4 stitetet |
| (4 4 4) |  4.4.4.4.4.4.4.4 osquat |
 3.4.3.4.3.4.3.4 osquat |
 4.4.4.4.4.4 osquat |
 4.8.4.8 teoct |
 4.8.4.8 teoct |
 4.8.4.8 teoct |
 8.8.8 ocat |
 3.4.3.4.3.4 dittitecat |
Symmetry mutations[edit]
(should really also add *333, but this is a start, from Mandara: The World of Uniform Tessellations
Families which contain only degenerate members (e.g. the quasitruncated {3,n}) are not shown; neither are those Wythoff symbols that already contain reducible fractions. Those that turn out to be degenerate anyway but do not satisfy either criterion are still shown. In some cases I have naughtily silently corrected the "doubled" constructions of the hemipolyhedra. Some of the Euclidean families involving {∞} correspond quite nicely to the hemipolyhedra, taking {∞} as an equator of r{4,4} or r{3,6}. However, some others do not have clear spherical analogues.
| *332 | *432 | *532 | *632 | *442 |
|---|---|---|---|---|
 3.3.3 tet 3 | 2 3 |
 4.4.4 cube 4 | 2 3 |
 5.5.5 doe 5 | 2 3 |
 6.6.6 hexat 6 | 2 3 |
 4.4.4.4 squat 4 | 2 4 |
 3.3.3 tet 3 | 2 3 |
 3.3.3.3 oct 3 | 2 4 |
 3.3.3.3.3 ike 3 | 2 5 |
 3.3.3.3.3.3 trat 3 | 2 6 |
 4.4.4.4 squat 4 | 2 4 |
 3.3.3.3 oct 2 | 3 3 |
 3.4.3.4 co 2 | 3 4 |
 3.5.3.5 id 2 | 3 5 |
 3.6.3.6 that 2 | 3 6 |
 4.4.4.4 squat 2 | 4 4 |
 3.4.3/2.4 thah 3 3/2 | 2 |
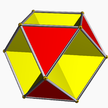 3.6.3/2.6 oho 3 3/2 | 3 |
 3.10.3/2.10 seihid 3 3/2 | 5 |
 3.∞.3/2.∞ tha 3 3/2 | ∞ |
 4.∞.4/3.∞ sha 4 4/3 | ∞ |
 3.4.3/2.4 thah 3 3/2 | 2 |
 4.6.4/3.6 cho 4 4/3 | 3 |
 5.10.5/4.10 sidhid 5 5/4 | 5 |
 6.∞.6/5.∞ hoha 6 6/5 | ∞ |
 4.∞.4/3.∞ sha 4 4/3 | ∞ |
 3.6.6 tut 2 3 | 3 |
 3.8.8 tic 2 3 | 4 |
 3.10.10 tid 2 3 | 5 |
 3.12.12 toxat 2 3 | 6 |
 4.8.8 tosquat 2 4 | 4 |
 3.6/2.6/2 3tet 2 3 | 3/2 |
 3.8/3.8/3 quith 2 3 | 4/3 |
 3.10/4.10/4 2sissid+gike 2 3 | 5/4 |
 3/2.12/5.12/5 quothat 2 3 | 6/5 |
 4/3.8/3.8/3 quitsquat 2 4 | 4/3 |
 3.6.6 tut 2 3 | 3 |
 4.6.6 toe 2 4 | 3 |
 5.6.6 ti 2 5 | 3 |
 6.6.6 hexat 2 6 | 3 |
 4.8.8 tosquat 2 4 | 4 |
 3.4.3.4 co 3 3 | 2 |
 3.4.4.4 sirco 3 4 | 2 |
 3.4.5.4 srid 3 5 | 2 |
 3.4.6.4 rothat 3 6 | 2 |
 4.4.4.4 squat 4 4 | 2 |
 3.6.3/2.6 oho 3/2 3 | 3 |
 4.8.3/2.8 socco 3/2 4 | 4 |
 5.10.3/2.10 saddid 3/2 5 | 5 |
 6.12.3/2.12 shothat 3/2 6 | 6 |
|
 4.6.4/3.6 cho 2 3 (3/2 3/2) | |
 4.8.4/3.8/7 sroh 2 3 (3/2 4/2) | |
 4.10.4/3.10/9 srid 2 3 (3/2 5/2) | |
 4.12.4/3.12/11 sraht 2 3 (3/2 6/2) | |
|
 3/2.4.3.4 thah 3/2 3 | 2 |
 3/2.4.4.4 querco 3/2 4 | 2 |
 3/2.4.5/4.4 (gicdatrid) 3/2 5 | 2 |
 3/2.4.6/5.4 qrothat 3/2 6 | 2 |
∞-covered {4} 4/3.4.4.4 4/3 4 | 2 |
 3.6/2.3.6/2 2oct 3 3 | 3/2 |
 3.8/3.4.8/3 gocco 3 4 | 4/3 |
 3.10/4.5.10/4 (sidtid+ditdid) 3 5 | 5/4 |
 3.12/5.6/5.12/5 ghothat 3 6 | 6/5 |
|
 4.8/3.4/3.8/5 groh 2 4/3 (3/2 4/2) | |
 4.12/5.4/3.12/7 graht 2 6/5 (3/2 6/2) | |
|||
 3.6.3/2.6 oho 3/2 3 | 3 |
 3.6.5/2.6 siid 5/2 3 | 3 |
|||
 3.8.4/3.8 socco 3 4/3 | 4 |
 3.10.5/3.10 sidditdid 3 5/3 | 5 |
|||
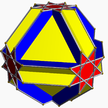 6.8.8/3 cotco 3 4 4/3 | |
 6.10.10/3 idtid 3 5 5/3 | |
|||
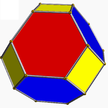 4.6.6 toe 2 3 3 | |
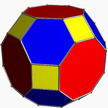 4.6.8 girco 2 3 4 | |
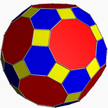 4.6.10 grid 2 3 5 | |
 4.6.12 othat 2 3 6 | |
 4.8.8 tosquat 2 4 4 | |
 4.6.6/2 cho+4{6/2} 2 3 3/2 | |
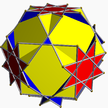 4.6/5.8/3 quitco 2 3 4/3 | |
 4.6.10/4 ri+12{10/4} 2 3 5/4 | |
 4.6/5.12/5 quitothit 2 3 6/5 | |
 4/3.8.8/5 qrasquit 2 4 4/3 | |
 6.6.6/2 2tut 3 3 3/2 | |
 6.8.8/3 cotco 3 4 4/3 | |
 6.10.10/4 siddy+12{10/4} 3 5 5/4 | |
 6.12/11.12/5 thotithit 3 6 6/5 | |
|
 12/5.6.12/5.∞ shaha 6 ∞ | 6/5 |
 8/3.4.8/3.∞ sossa 4 ∞ | 4/3 | |||
 12.6/5.12.∞ ghaha 6/5 ∞ | 6 |
 8.4/3.8.∞ gossa 4/3 ∞ | 4 | |||
 12/5.12.12/7.12/11 huht 6/5 6 (6/2 ∞/2) | |
 8/3.8.8/5.8/7 sost 4/3 4 (4/2 ∞/2) | | |||
 12.12/5.∞ hatha 6/5 6 ∞ | |
 8.8/3.∞ satsa 4/3 4 ∞ | | |||
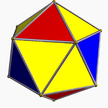 3.3.3.3.3 ike | 2 3 3 |
 3.3.3.3.4 snic | 2 3 4 |
 3.3.3.3.5 snid | 2 3 5 |
 3.3.3.3.6 snathat | 2 3 6 |
 3.3.4.3.4 snasquat | 2 3 4 |
 (3.3.3.3.3)/2 gike | 2 3/2 3/2 |
 3.3.4/3.3.4/3 rasisquat | 2 4/3 4/3 | |||
 3.4.3.4/3.3.∞ snassa | 4 4/3 ∞ |
References[edit]
Klitzing:
McNeill:
- ^ Coxeter, Regular Polytopes, p. 114
